命题“
∈N，x02 +2xo≥3”的否定为（）
| A．∈N，x02 +2x0≤3 |
B． ∈N ，x2+2x≤3 |
| C．∈N，x02 +2x0＜3 |
| D．∈N，x2+2x＜3 |
已知全集U=R，集合A={x|x≥
}，集合B={x|x≤l}，那么
（）
| A．{x|x≤或x≥1} |
| B．{x|x＜或x＞1） |
| C．{x|＜x＜1} |
| D．{x|≤x≤l} |
已知定义在
上的可导函数
的导函数为
（x），满足
，且
为偶函数，
，则不等式
的解集为（）
A．（-2，+ ） |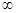
B．（0．+） |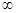
C．（1， ） |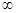
D．（4，+） |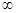
是定义在
上的奇函数，且当
时，
，则函数的零点的个数是（）
A． |
B． |
C． |
D． |
已知函数
，若
中，角C是钝角，那么（ ）
A． |
B． |
C． |
| D． |
满足
，则当
时，
（ ）
