如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。 小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……,如此继续,得到一系列点P1,P2,P3,…,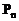 。 若
。 若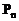 与P重合,则n的最小值是 ( )
与P重合,则n的最小值是 ( )
| A.5 | B.6 | C.7 | D.8 |
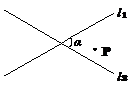
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点。已知BC=24cm,则这个展开图可折成的正方体的体积为()
| A.64cm3 | B.27cm3 | C.9cm3 | D.8cm3 |
若关于x的方程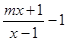 =0无解,则()
=0无解,则()
| A.m=1 | B.m=﹣1 | C.m=0或﹣1 | D.m=1或﹣1 |
如图,在ABC中,AD平分∠BAC,AE:AC=AF:AB=1:3,那么AG:GD的值为()
| A.1:2 | B.1:3 | C.2:5 | D.3:5 |
下列命题是真命题的是()
| A.相等的角是对顶角 |
| B.三角形的一个外角大于任何一个内角 |
| C.一组邻边对应成比例的两个矩形相似 |
D.若AB被点C黄金分割,则AC=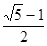 AB AB |
如图,能使BF∥DG的条件是()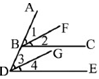
| A.∠1=∠3 | B.∠2=∠4 | C.∠2=∠3 | D.∠1=∠4 |