某市出租汽车收费标准如下：3千米以内（含3千米）收费8元；超过3千米的部分，每千米收费1.4元。
（1）写出应收车费y（元）与出租汽车行驶路程x（千米）之间的函数关系式。
（2）小明乘坐出租车行驶4千米应付多少元？
（3）若小华付车费19.2元，则出租车行驶了多少千米？
如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A（0，2），B（4，2）C
（6，0），解答下列问题：
（1）请在图中确定该圆弧所在圆心D点的位置，则D点坐标为________ ；
（2）连结AD，CD，求⊙D的半径（结果保留根号）；
（3）求扇形DAC的面积. （结果保留π）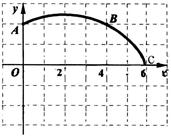
初中生对待学习的态度一直是教育工作者关注的问题之一．为此，某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计该区近20000名初中生中大
约有多少名学生学习态度达标（达标包括A级和B级）？
如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是
30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪
的高度是1.5m，请你计算出该建筑物的高度．（取
＝1.732，结果精确到1m）
如图，已知平行四边形ABCD中，点
为
边的中点，延长
相交于点
．
求证：
．
计算：