如图所示,已知△ABD≌△ACE,∠B=∠C,试指出这两个三角形的对应边和对应角. 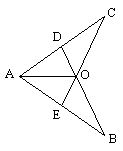
如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.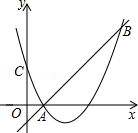
如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的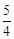 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)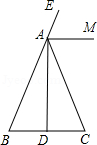
已知:直角坐标系xoy中,将直线 沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线
沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线 与
与 轴交于A,B两点(点A在点B的右侧),且经过点C,
轴交于A,B两点(点A在点B的右侧),且经过点C,
(1)求直线 的解析式;
的解析式;
(2)求抛物线的解析式;
(3)设抛物线的顶点为 ,点
,点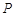 在抛物线的对称轴上,且
在抛物线的对称轴上,且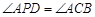 ,求点
,求点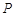 的坐标;
的坐标;