我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下，它们会全等?
（1）阅读与证明：
对于这两个三角形均为直角三角形，显然它们全等.
对于这两个三角形均为钝角三角形，可证它们全等（证明略）.
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
已知：△ABC、△A1B1C1均为锐角三角形，AB＝A1B1，BC＝B1C1，∠C＝∠C1.
求证：△ABC≌△A1B1C1. （请你将下列证明过程补充完整）
证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1.
则∠BDC＝∠B1D1C1＝90°，
∵BC＝B1C1，∠C＝∠C1，
∴△BCD≌△B1C1D1，
∴BD＝B1D1.
______________________________。
（2）归纳与叙述：
由（1）可得到一个正确结论，请你写出这个结论.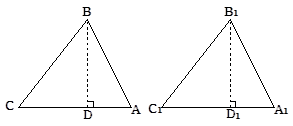 
如图所示，一段街道的两边缘所在直线分别为AB、PQ，并且AB∥PQ．建筑物的一端DE所在的
直线MN⊥AB于点M，交PQ于点N．小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等
候小亮．
（1）请你在图中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置（用点C标出）；
（2）已知：MN=20m，MD=8m，PN=24m，求（1）中的点C到胜利街口的距离CM．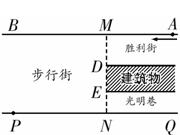
某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．
（1）写出所有选购方案(利用树状图或列表方法表示)；
（2）如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？
（3）现知希望中学购买甲、乙两种品牌电脑共36台(价格如图20所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．
解方程：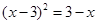
计算：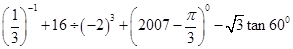
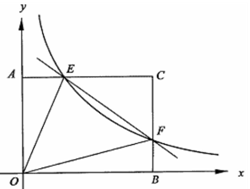
已知：在矩形A0BC中，分别以OB，OA所在直线为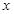
轴和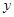
轴，建立如图所示的平面直角坐标系．E是边AC上的一个动点（不与A，C重合），过E点的反比例函数
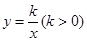的图象与BC边交于点F．
（1）若△OAE、△OBF的面积分别为S1、S2且S1+S2=2，求k的值；
（2）若OB=4，OA=3，记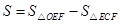
问当点E运动到什么位置时，S有最大值，其最大值为多少？
（3）请探索：是否存在这样的点E，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，求出点E的坐标；若不存在，请说明理由．