利用“等积”计算或说理是一种很巧妙的方法， 就是一个面积从两个不同的角度表示。如图甲，已知Rt△ABC中，∠C=90°，CD⊥AB于D，BC=3,AC=4,求CD的长。
解题思路：利用勾股定理易得AB=5利用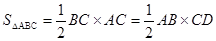
，可得到CD=2.4
请你利用上述方法解答下面问题：
（1） 如图甲，已知Rt△ABC中，∠C=90°，CD⊥AB于D，BC=5,AC=12,求CD的长。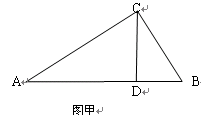
(2)如图乙，△ABC是边长为2的等边三角形，点D是BC边上的
任意一点，DE⊥AB于E点，DF⊥AC于F点，求DE+DF的值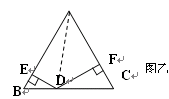
如图，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，若AC＝6，BC＝8，CD＝3．
(1)求DE的长；
(2)求△ADB的面积．
一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法，如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB＝a，BC＝b，AC＝c．请利用四边形BCC′D′的面积证明勾股定理．
如图，A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC＝1km，BD＝3km，且CD＝3km，现要在河边上建一个水厂向A、B两村输送自来水，铺设水管的费用为20000元／km，请你在CD上选择水厂位置O，使铺设水管的费用最低，并求出铺设水管的总费用．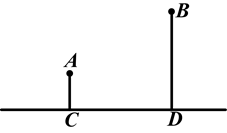
如图所示，在长方形ABCD中，AB＝8，BC＝4，将长方形沿AC折叠，使点D落在点D′处，求重叠部分△AFC的面积．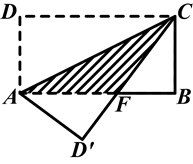
如图，在四边形ABCD中，AB＝2，CD＝1，∠A＝60°，∠B＝∠D＝90°，求四边形ABCD的面积．