如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°,AB＝BC, E为AB边上一点，∠BCE＝
15°，AE＝AD．连接DE、AC交于F，连接BF．则有下列3个结论：①
②△ACD≌△ACE； ③ △CDE为等边三角形,其中正确的结论是 （ ） 
A．①② B．①③ C．③ D．①②③
如图，点P为∠AOB内一点，分别作出点P关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N，若P1P2=6，则△PMN的周长为（ ）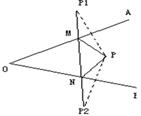
A、4 B、5 C、6 D、7
如图所示，已知△ABC中，∠BAC=90°，AB=AC，∠BAD=30°，AD=AE，则∠EDC的度数为（ ）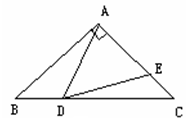
| A．10° | B．15° | C．20° | D．30° |
画∠AOB的角平分线的方法步骤是：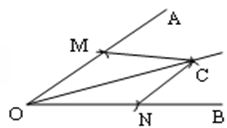
①以O为圆心，适当长为半径作弧，交OA于M点，交OB于N点；
②分别以M、N为圆心，大于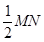
的长为半径作弧，两弧在∠AOB的内部相交于点C；
③过点C作射线OC.射线OC就是∠AOB的角平分线。这样作角平分线的根据是 ( )
A、SSS B、SAS C、ASA D、AAS
已知:如图，AC=AE，∠1=∠2，AB=AD，若∠D=25°，则∠B的度数为 ( )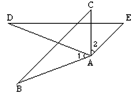
| A．25° | B．30° | C．15° | D．30°或15° |
已知等腰三角形的两边长分别为4cm、8cm，则该等腰三角形的周长是（）
| A．12cm | B．16cm | C．16cm或20cm | D．20cm |