“嫦娥一号”探月卫星与稍早前日本的“月亮女神号”探月卫星不同，“嫦娥一号”卫星是绕月极地轨道上运动的加上月球的自转，因而“嫦娥一号”卫星能探测到整个月球的表面。12月11日“嫦娥一号”卫星CCD相机已对月球表面进行成像探测，并获取了月球背面部分区域的影像图。卫星在绕月极地轨道上做圆周运动时距月球表面高为H，绕行的周期为TM；月球地公转的周期为TE，半径为R0。地球半径为RE，月球半径为RM。试解答下列问题：
（1）若忽略地球及太阳引力对绕月卫星的影响，试求月球与地球质量之比；
（2）当绕月极地轨道的平面与月球绕地公转的轨道平面垂直，也与地心到月心的连线垂直（如图所示）。此时探月卫星向地球发送所拍摄的照片，此照片由探月卫星传送到地球最少需要多长时间？已知光速为c。
如图所示，物块Α、Β用一劲度系数为k=200N/m的轻弹簧相连静止于水平地面上，Α物体质量mA=2kg， Β物体质量mB="4Kg." 现用一恒力F=30N竖直向上拉物体A， 使Α从静止开始运动，当Α运动到最高点时Β刚好要离开地面但不能继续上升。若弹簧始终处于弹性限度内，取g = 10m/s2。求：
（1）Β刚要离开地面时，拉力F做的功；
（2）Β刚要离开地面时Α的加速度大小；
（3）从Α开始运动到Α到达最高点的过程中弹簧弹力对Α做的功。
如图所示，底座A上装有L=0.5m长的的直立杆，底座和杆的总质量为M=1.0kg，底座高度不计，杆上套有质量为m=0.2kg的小环B，小环与杆之间有大小恒定的摩擦力。当小环从底座上以v0=4.0m/s的初速度向上飞起时，恰好能到达杆顶，然后沿杆下降，取g=10m/s2，求：
①在环飞起过程中，底座对水平面的压力；
②此环下降过程需要多长时间。
如图，BC为半径等于Ｒ＝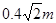
竖直放置的光滑细圆管，O为细圆管的圆心，BO与竖直线的夹角为45°；在圆管的末端C连接一光滑水平面，水平面上一质量为Ｍ＝1.5kg的木块与一轻质弹簧拴接，轻弹簧的另一端固定于竖直墙壁上．现有一质量为m=0.5kg的小球从Ｏ点正上方某处Ａ点以v0水平抛出，恰好能垂直OB从B点进入细圆管，小球从进入圆管开始即受到始终竖直向上的力F=5N的作用，当小球运动到圆管的末端C时作用力F立即消失．小球过后与木块发生完全非弹性碰撞（g=10m/s2）．求：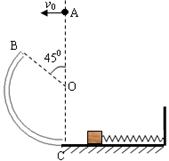
（1）小球在Ａ点水平抛出的初速度v0；
（2）在圆管运动中圆管对小球的支持力Ｎ；
（3）弹簧的最大弹性势能ＥＰ．
如图，粗糙水平面与半径R=1.5m的光滑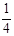
圆弧轨道相切于B点，质量m=1kg的物体在大小为10N、方向与水平水平面成37°角的拉力F作用下从A点由静止开始沿水平面运动，到达B点时立刻撤去F，物体沿光滑圆弧向上冲并越过C点，然后返回经过B处的速度vB=15m/s。已知sAB=15m，g=10m/s2，sin37°=0.6，con37°=0.8。求：
（1）物体到达C点时对轨道的压力；
（2）物体越过C点后上升的最大高度h。
（3）物体与水平面的动摩擦因数μ。
A,B两车沿同一直线同方向运动，A车的速度vA="4" m/s,B车的速度vB="10" m/s.当B车运动至A车前方7 m处时，B车刹车并以a="2" m/s2的加速度做匀减速运动，从该时刻开始计时，求：
（1）A车追上B车之前，二车间的最大距离；
（2）经多长时间A车追上B车。