电磁炉专用平底锅的锅底和锅壁均由耐高温绝缘材料制成.起加热作用的是安在锅底的一系列半径不同的同心导电环.导电环所用的材料单位长度的电阻R=0.125 Ω/m,从中心向外第n个同心圆环的半径为rn="(2n-1)" r1(n为正整数且n≤7),已知r1="1.0" cm.当电磁炉开启后,能产生垂直于锅底方向的变化磁场,已知该磁场的磁感应强度B的变化率为
Ω/m,从中心向外第n个同心圆环的半径为rn="(2n-1)" r1(n为正整数且n≤7),已知r1="1.0" cm.当电磁炉开启后,能产生垂直于锅底方向的变化磁场,已知该磁场的磁感应强度B的变化率为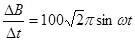 ,忽略同心导电圆环感应电流之间的相互影响.
,忽略同心导电圆环感应电流之间的相互影响.
(1)半径为r1的导电圆环中感应电流的最大值I1m是多大?(计算中可取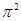 ="10" )
="10" )
(2)假设导电圆环的热全部以波长为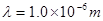 的红外线光子辐射出来,那么半径为
的红外线光子辐射出来,那么半径为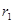 的导电圆环上每分钟辐射出去的光子数是多少?
的导电圆环上每分钟辐射出去的光子数是多少?
(3)若不计其他损失,所有导电圆环的总功率P是多大?
如图所示,离子发生器发射一束质量为m,电荷量为+q的离子,从静止经PQ两板间的加速电压加速后,以初速度v0再从a点沿ab方向进入一匀强电场区域,abcd所围成的正方形区域是该匀强电场的边界,已知正方形的边长为L,匀强电场的方向与ad边平行且由a指向d.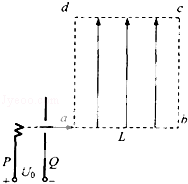
(1)求加速电压U0;
(2)若离子恰从c点飞离电场,求ac两点间的电势差Uac;
(3)若离子从边界上某点飞出时的动能为mv02,试判断离子从哪条边界飞出,并求此时匀强电场的场强大小E.
如图所示,电阻R1=8Ω,电动机绕组电阻R0=2Ω,当开关S断开时,电阻R1消耗的电功率是2.88W;当开关S闭合时,电阻R1消耗的电功率是2W.若电源的电动势为6V,求开关S闭合时
(1)干路中的总电流
(2)电动机输出的机械功率.
(3)若此电动机输出的机械功率不变,用它从静止开始竖直提升0.5Kg 物体时,物体匀速上升时的速度为多大.(g=10m/s2)
如图所示,匀强电场中A、B、C三点构成一个直角三角形中,∠A=30°,边长AC=32 cm.把电荷量q=﹣2×10﹣10C的点电荷由A点移到B点,电场力做功4.8×10﹣8J,再由B点移到C点,电荷克服电场力做功4.8×10﹣8J,取B点的电势为零,求
cm.把电荷量q=﹣2×10﹣10C的点电荷由A点移到B点,电场力做功4.8×10﹣8J,再由B点移到C点,电荷克服电场力做功4.8×10﹣8J,取B点的电势为零,求
(1)A、C两点的电势;
(2)匀强电场的场强.
如图,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为r,在a点处固定一电荷量为q(q>0)的点电荷.一同学将一检测电荷沿直线在ac间移动时发现只在b点不需加力.不计重力,已知静电力常量为K.求d点处场强的大小.
正以30m/s的速率运行的列车,接到前方小站的请求:接一垂危病人上车.列车先以加速度大小0.6m/s2做匀减速运动,恰到该小站停止,停车lmin后再以1.0m/s2的加速度匀加速直线启动,直到恢复原速行驶.(列车始终沿直线运动),求:
(1)该列车匀减速运动到停车走了多少位移.
(2)该列车由于临时停车,共耽误多长时间.