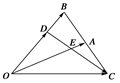
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB= OB,DC与OA交于点E,设
OB,DC与OA交于点E,设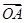 =a,
=a, =b,用a,b表示向量
=b,用a,b表示向量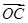 ,
,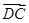 .
.
(本题满分12分)一个袋中装有四个形状大小完全相同的球,球的编号分别为 ,
,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于 的概率;
的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,
,将球放回袋中, 然后再从袋中随机取一个球,该球的编号为
然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.
(本题满分12分)在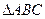 中,
中,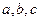 分别是角
分别是角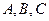 的对边,向量
的对边,向量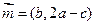 ,
,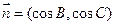 ,且
,且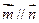 .
.
(Ⅰ)求角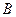 的大小;
的大小;
(Ⅱ)设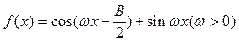 ,且
,且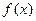 的最小正周期为
的最小正周期为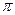 ,求
,求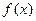 在区间
在区间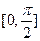 上的最大值和最小值.
上的最大值和最小值.
(本题满分12分)已知数列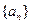 是一个等差数列,其前
是一个等差数列,其前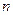 项和为
项和为 ,且
,且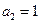 ,
,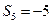 .
.
(Ⅰ)求通项公式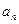 ;
;
(Ⅱ)求数列前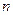 项和
项和 ,并求出
,并求出 的最大值.
的最大值.
(Ⅲ)求数列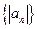 的前
的前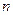 项和
项和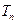 .
.
(本小题满分12分)实系数方程 的一个根在(0,1)内,另一个根在(1,2)内,求:
的一个根在(0,1)内,另一个根在(1,2)内,求:
(1)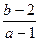 的取值范围;
的取值范围;
(2)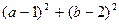 的取值范围;
的取值范围;
(3)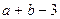 的取值范围.
的取值范围.
(本小题满分12分)制定投资计划时,不仅要考虑可能获得的赢利,而且要考虑
可能出现的亏损。某投资人打算投资甲、乙两个项目 ,根据预测,甲、乙项目可能的最大
,根据预测,甲、乙项目可能的最大
赢利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额
不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投 资人对甲、乙两个项目各
资人对甲、乙两个项目各
投资多少万元,才能使可能的赢利最大?