阅读材料:我们知道|x|的几何意义是在数轴上的数x对应的点与原点的距离,即|x|=|x-0|,也就是说|x|表示在数轴上数x与数0对应的点之间的距离。这个结论可以推广为|x1-x2|表示在数轴上数x1与x2对应的点之间的距离。
例1:已知|x|=2,求x的值。
解:容易看出,在数轴上与原点的距离为2的点对应的数为-2和2,即x的值为-2和2。
例2:已知|x-1|=2,求x的值。
解:在数轴上与数1对应的点之间的距离为2的点对应的数为3和-1,即x的值为3和-1。
仿照阅读材料的解法,求下列各式中的x的值。
(1)|x|=3 (2)|x+2|=4
求不等式: 的最大整数解
的最大整数解
如图①,直线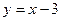 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且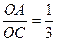 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.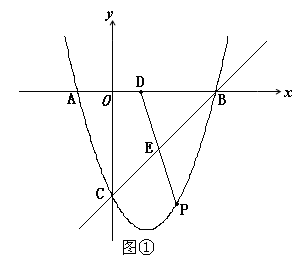
(1)写出A、B、C三点的坐标,并求抛物线的解析式;
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。
如图,⊙O的半径为5cm, AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求线段BC的长度.
某电器城购进一批单价为8元的节能灯管,如果按每支10元出售,那么每天可销售100支,经调查发现,这种节能灯管的售价每提高1元,其销售量相应减少5支,为了每天获得最大利润,该电器城应将这种灯管的售价定为每支多少元?每天获得的最大利润是多少?
如图,在△ 中,∠A=45°,
中,∠A=45°, ,
, cm,求AB的长度
cm,求AB的长度