如图,等腰梯形ABCD中,AB//CD,DC=AD=BC,且对角线AC垂直于腰BC,求梯形的各个内角.
(1)解不等式3x-2≥4,并将解集在数轴上表示出来.
(2)化简:
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠
在两坐标轴上,点C为 (-1,0).如图所示,B点在抛物线y=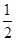 x2+
x2+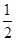 x-2图象上,过点B作
x-2图象上,过点B作
BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所
有点P的坐标;若不存在,请说明理由.
如图,在平面直角坐标xOy中,一次函数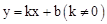 的图象与反比例函数
的图象与反比例函数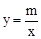 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6, ).线段OA=5,E为x轴上一点,且sin∠AOE=
).线段OA=5,E为x轴上一点,且sin∠AOE= .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2,
(1)求CD的长;
(2)求BF的长.