以下时某同学课题学习实习报告的一部分
实习报告
| 题目 |
了解当地8年级男生的身高情况 |
|||||||||||
| 具体要求 |
从其中的一个学校选取容量为60的样本,计算样本平均数去估计总平均数;列频数分布表,绘制频数分布直方图 |
|||||||||||
| 样本来源 |
当地某中学 |
样本容量 |
60 |
|||||||||
| 获取样本 的方法 |
将八年级男生一次编上号1~180,通过抽签得到60名男生的编号,到校有关部门查阅他们的身体检查表,抄录其身高数据 |
|||||||||||
| 样本数据(单位:cm) |
158 |
163 |
160 |
175 |
167 |
165 |
172 |
155 |
158 |
164 |
||
| 170 |
166 |
148 |
164 |
171 |
166 |
165 |
162 |
159 |
179 |
|||
| 170 |
163 |
164 |
157 |
155 |
163 |
166 |
169 |
163 |
163 |
|||
| 171 |
161 |
166 |
165 |
164 |
167 |
169 |
172 |
173 |
154 |
|||
| 149 |
169 |
163 |
161 |
163 |
166 |
164 |
177 |
163 |
150 |
|||
| 162 |
163 |
154 |
166 |
170 |
166 |
159 |
161 |
166 |
158 |
|||
| 数据整理 与分析 |
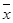 样本=164cm 样本=164cm |
|||||||||||
| 分组 |
频数 |
百分比 |
||||||||||
| 147.5~151.5 |
3 |
5% |
||||||||||
| 151.5~155.5 |
4 |
6.7% |
||||||||||
| 155.5~159.5 |
|
10% |
||||||||||
| 159.5~163.5 |
15 |
|
||||||||||
| 163.5~167.5 |
|
30% |
||||||||||
| 167.5~171.5 |
8 |
13.3% |
||||||||||
| 171.5~175.5 |
4 |
6.7% |
||||||||||
| 175.5~179.5 |
2 |
3.3% |
||||||||||
| 合计 |
60 |
|
||||||||||
请你阅读以上实习报告,解答下列问题:
(1)请你填写实习报告中未完成的4个数据;
(2)试估计该校八年级男生的平均身高;
(3)在这个问题中,总体和样本各指什么?
(4)该校八年级男生身高在171.5cm以上的人数约为多少?占多大比例?
(5)绘制八年级男生身高频数分布直方图。
(1)计算: ;
(2)解不等式组: .
如图,已知抛物线 过点 , , ,其顶点为 .
(1)求抛物线的解析式;
(2)设点 ,当 的值最小时,求 的值;
(3)若 是抛物线上位于直线 上方的一个动点,求 的面积的最大值;
(4)若抛物线的对称轴与直线 相交于点 , 为直线 上任意一点,过点 作 交抛物线于点 ,以 , , , 为顶点的四边形能否为平行四边形?若能,求点 的坐标;若不能,请说明理由.
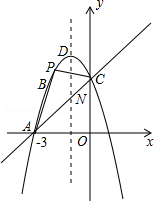
如图,在 中,直径 经过弦 的中点 ,点 在 上, 的延长线交 于点 ,交过 的直线于 , ,连接 与 交于点 .
(1)求证: 是 的切线;
(2)若点 是 的中点, 的半径为3, ,求 的长.

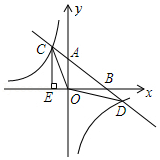
如图,一次函数 的图象与反比例函数 的图象交于 , 两点,与 , 轴交于 , 两点,且 , , ,作 轴于 点.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求 的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量 的取值范围.
某市教育局对某镇实施“教育精准扶贫”,为某镇建中、小型两种图书室共30个.计划养殖类图书不超过2000本,种植类图书不超过1600本.已知组建一个中型图书室需养殖类图书80本,种植类图书50本;组建一个小型图书室需养殖类图书30本,种植类图书60本.
(1)符合题意的组建方案有几种?请写出具体的组建方案;
(2)若组建一个中型图书室的费用是2000元,组建一个小型图书室的费用是1500元,哪种方案费用最低,最低费用是多少元?