某公司有15名员工,它们所在的部门及相应每人所创的年利润如下表示
| 部门 |
A |
B |
C |
D |
E |
F |
G |
| 人数 |
1 |
1 |
2 |
4 |
2 |
2 |
3 |
| 每人所创的年利润 |
20 |
5 |
2.5 |
2.1 |
1.5 |
1.5 |
1.2 |
根据表中的信息填空:
(1) 该公司每人所创年利润的平均数是 万元.
(2) 该公司每人所创年利润的中位数是 万元.
(3) 你认为应该使用平均数和中位数中哪一个来描述该公司每人所创年利润的一般水平?
答
如图,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.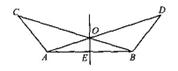
如图,∠A=55°,∠B=30°,∠C=35°,求∠BDC的度数.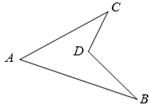
在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).
(1)在图中作出△ABC关于y轴的对称△A1B1C1.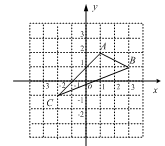
(2)写出△ABC关于x轴对称△A2 B2C2的各顶点坐标.
A2 ______________
B2 ______________
C2______________
a、b、c在数轴上的位置如图所示,则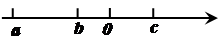
(1)用“>、<、=”填空: ,
, ,
,
(2)用“>、<、=”填空: ,
, 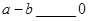 ,
,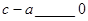
(3)化简: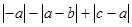
出租车司机老王某天上午营运全是在东西走向的解放路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
将第几名乘客送到目的地时,老王刚好回到上午出发点?
将最后一名乘客送到目的地时,老王距上午出发点多远?
若汽车耗油量为0.4L/km,这天上午老王耗油多少升?