阅读下面的情境对话，然后解答问题
（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？
（2）在Rt
ABC 中， ∠ACB＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若RtABC是奇异三角形，求a：b：c；
（3）如图，AB是⊙O的直径，C是上一点（不与点A、B重合），D是半圆的中点，CD在直径AB的两侧，若在⊙O内存在点E使得AE＝AD，CB＝CE．
1求证：ACE是奇异三角形；
2当ACE是直角三角形时，求∠AOC的度数．
已知：如图，在△BAC中，AB=AC，D、E分别是AB、AC的中点，且CD=BE．
求证：∠ADC=∠AEB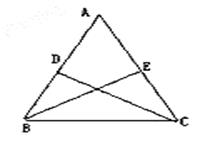
先化简，再求值:（x+y）（x-y）+（4x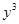
-8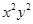
）÷4xy，其中x=2，y=1
把下列多项式分解因式．
（1）
-2
y+x
（2）4x-16
计算：
（1）20152-2016×2014
（2）（x4-2x2y2）÷x2-（x+y）2
阅读理解：如图，A．B．C为数轴上三点，若点C到A的距离是点C到B的距离的2倍，我们就称点C是【A，B】的好点．例如，如图1，点A表示的数为－1，点B表示的数为2．表示数1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点；又如，表示数0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A，B】的好点，但点D是【B，A】的好点．
知识运用：如图2，M、N为数轴上两点，点M所表示的数为－2，点N所表示的数为4．
（1）数 所表示的点是【M，N】的好点；
（2）现有一只电子蚂蚁P从点N出发，以每秒2个单位的速度沿数轴向左运动，运动时间为t．当t为何值时，P、M、N中恰有一个点为其余两点的好点？