两人要去某风景区游玩,每天某—时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆乍的状况比第一辆好,他就上第二辆车;如果第二辆不比第—辆好,他就上第三辆车.若把这三辆车的舒适程度分为上、中、下三等.请问:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
如下图,在四边形ABCD中,AC、BD交于点0,AC=BD,E、F分别是AB、CD中点,EF分别交AC、BD于点H、G。求证:OG=OH。
已知:如图,在梯形ABCD中,AD//BC,AB⊥BC,E是CD中点,试问:线段AE和BE之间有怎样的大小关系?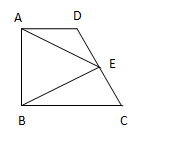
如图,在梯形ABCD中,AD//BC,∠B=50°,∠C=80°,AD=2,BC=5,求CD的长。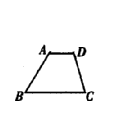
如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.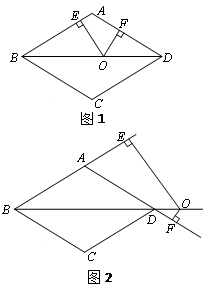
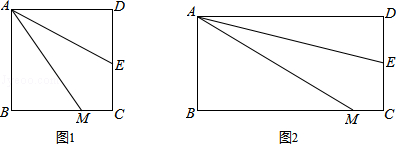
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.