如图所示，在铅板A上有一个发射源C，可向各个方向射出速率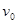
=2.8×106m/s的电子，B为金属网，A、B连接在电路上，电源电动势E=20V，内阻不计，滑动变阻器范围为0~20Ω， A、B间距d=10cm，M为荧光屏(足够大)，它紧挨着金属网外侧，已知电子的比荷
，现将图中滑动变阻器滑片
置于Rap=5.6Ω，闭合开关后，求：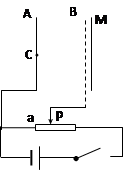
⑴ A、B间场强大小；
⑵ 不同方向射出的电子到达荧光屏的时间不同，则电子到达
荧光屏的最长时间和电子到达荧光屏范围的最大宽度是多少；
⑶ 调节R使粒子打在荧光屏上面积范围缩小为原来一半，
此时调节Rap至多大？
如图所示，用同样材料制成的一个轨道，AB段为1/4圆弧，半径为R=2m，水平放置的BC段长度也为R，一小物块质量为m=1Kg，与轨道间动摩擦因数为µ=0.2，当它从轨道顶端A由静止下滑时，恰好运动到C点静止，求物体在AB段克服摩擦力所做的功。（取g=10m/s2）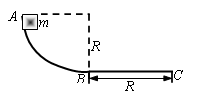
某消防员在一次执行任务过程中，从10 m长的直杆顶端从静止开始匀加速下滑，加速度大小a1＝8 m/s2，然后立即匀减速下滑，减速时加速度大小a2＝4 m/s2，落地时速度不许超过4 m/s，把消防员看成质点，求下滑全过程最短时间．
如图所示，A、B两球放在光滑的水平面上，水平面的右侧与竖直平面内一光滑曲面相切，现给A一向右的速度，让A与B发生对心弹性碰撞，小球沿曲面上升到最高点后又能再沿曲面滑回到水平面。若要B返回水平面时能再与么发生碰撞， A、B的质量应满足什么关系？
某学校科技小组对一辆自制小遥控车的性能进行研究，他们让小车在水平地面上由静止开始运动，并将小车运动的全过程记录下来，通过数据处理得到如图所示的v-t图像，已知小车在0-2s内做匀加速直线运动，2-10s内小车牵引力的功率保持不变，在10s末停止遥控，关闭电动机。小车的质量m=1kg，整个过程中小车受到的阻力保持不变。求：
（1）小车所受的阻力f；
（2）小车在2-10s内牵引力的功率；
（3）小车在14s内阻力f做的功。
有一质量为0.2kg的物块，从长为4m，倾角为30°的光滑斜面顶端处由静止开始滑下，斜面底端和水平面的接触处为很短的圆弧形，如图所示，物块和水平面间的动摩擦因数为0.2(g取10m／s2)，求：
(1)物块到达斜面底端时的速度；
(2)物块在水平面能滑行的距离。