某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶记录如下(单位:千米)
+10,-9,+7,-15,+6,-14,+4,-2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示，请在原图上利用尺规作图作出音乐喷泉M的位置，（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）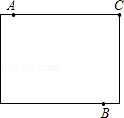
化简：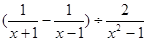
已知点A(1，c)和点B (3，d )是直线y＝k1x＋b与双曲线y＝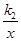
（k2＞0）的交
点．
（1）过点A作AM⊥x轴，垂足为M，连结BM．若AM＝BM，求点B的坐标；
（2）设点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线y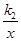＝（k2＞0）于点N．当 
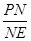取最大值时，若PN＝ 
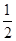，求此时双曲线的解析式．
已知
ABCD，对角线AC与BD相交于点O，点P在边AD上，过点P分
别作PE⊥AC、PF⊥BD，垂足分别为E、F，PE＝PF．
（1）如图，若PE＝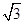
，EO＝1，求∠EPF的度数；
（2）若点P是AD的中点，点F是DO的中点，BF ＝BC＋3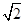
－4，求BC的长．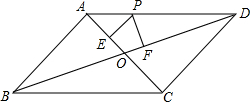
如图，在平面直角坐标系中，已知点A(2，3)、B(6，3)，连结AB. 如果点P
在直线y＝x－1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．
（1）判断点Ｃ(
，
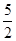) 是否是线段AB的“邻近点”，并说明理由；
（2）若点Q (m，n)是线段AB的“邻近点”，求m的取值范围．