观察图和所给表格中的各数后再回答问题:
| 梯形个数 |
1 |
2 |
3 |
4 |
5 |
| 图形周长 |
5 |
8 |
11 |
14 |
17 |
当梯形个数为n时,这个图形的周长是多少?
如图,已知一次函数y=kx+b的图象交反比例函数 的图像交于点A、B,交x轴于点C.
的图像交于点A、B,交x轴于点C.求m的取值范围;
若点A的坐标是(2,-4),且
 ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;根据图像,写出当反比例函数的值小于一次函数的值时x 的取值范围?

某工程限期完成,甲队独做正好按期完成,乙队独做则要误期3天,两队合做2天后,其余工程再由乙队独做, 正好按期完成.该工程的限期是多少天?
有三张背面完全相同的卡片,它们的正面分别写上 ,
, ,
, ,把它们的背面朝上洗匀后,小丽先从中抽取一张,然后小明从余下的卡片中再抽取一张.
,把它们的背面朝上洗匀后,小丽先从中抽取一张,然后小明从余下的卡片中再抽取一张.小丽取出的卡片恰好是
 概率是______________;
概率是______________;小刚为他们设计了一个游戏规则:若两人抽取卡片上的数字之积是有理数,则小丽获胜;否则小明获胜.你认为这个游戏规则公平吗?若不公平,则对谁有利?请用画树状图或列表法进行分析说明,并为他们设计一个公平的游戏规则.
如图,一条小“鱼”的头部点O的坐标为(0,0),其鱼鳍部位点A的坐标为(3,2).请以点O为位似中心,在方格中画出一条大鱼与小鱼成位似图形,且位似比为2;
在你所画的图中找出与点A对应的点,记为A’,则点A’的坐标为____________.
两个立体图形的体积比是其相似比的立方,如两个立方体的体积之比为两立方体棱长之比的立方.根据这个结论可知:若小鱼的质量为1kg,则大鱼的质量大约为_________kg.

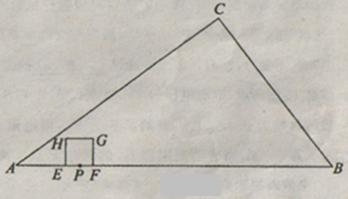
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立即以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.当t=1时,正方形EFGH的边长是;
当t=3时,正方形EFGH的边长是;当0<t≤2时,求S与t的函数关系式;
直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?