一人通过箱带拉着一个旅行箱前进,拉力是12 N,箱带与水平面夹角是30°,则拉力的水平分力是多大?竖直分力是多大?
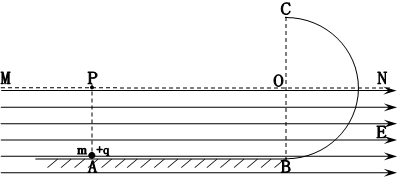
如图所示,光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接。在过圆心O的水平界面的下方分布有水平向右的匀强电场。现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动到C之前电量保持不变,经过C点后电量立即变为零)。已知A、B间的距离为2R,重力加速度为g。在上述运动过程中,
|
|

质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒悬停在空间范围足够大的匀强电场中,电场强度大小为E1.在t=0时刻,电场强度突然增加到E2=4.0×103N/C,场强方向保持不变.到t=0.20s时刻再把电场方向改为水平向右,场强大小保持不变.取g=10m/s2.求:
(1)原来电场强度E1的大小?
(2)t=0.20s时刻带电微粒的速度大小?
(3)带电微粒运动速度水平向右时刻的动能?
“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时江汉大学的500名学生将担任司机,负责接送比赛选手和运输器材。在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F— 图象(图中AB、BO均为直线))。假设电动车行驶中所受的阻力恒定,
图象(图中AB、BO均为直线))。假设电动车行驶中所受的阻力恒定,
求此过程中(1)电动车的额定功率;
(2)电动车由静止开始运动,经过多长时间,速度达到2m/s?
酒后驾车严重威胁交通安全。饮酒后会使人的反应时间(从发现情况到实施作制动的时间)变长,造成反制距离(从发现情况到汽车停止的距离)变长。假定汽车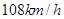 的速度匀速行驶,刹车时汽车的加速度大小是
的速度匀速行驶,刹车时汽车的加速度大小是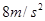 ,正常人的反应时间为
,正常人的反应时间为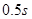 ,饮酒人的反应时间为
,饮酒人的反应时间为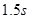 .
.
问:(1)驾驶员饮酒后的反制距离比正常时多几米?
(2)饮酒的驾驶员从发现情况到汽车停止需多少时间?
汽车从静止开始以a=1m/s2的加速度直线前进,车前与车相距x0=20m处,某人同时开始以4m/s的速度同方向匀速向前运动。
(1)经过多长时间汽车的速度达到4m/s?
(2)汽车追上人之前,他们之间的最大间距是多少?
(3)经过多长时间车才追上人?