(本小题满分14分) 如图，已知抛物线与坐标轴分别交于A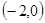
、B
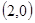、C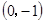
三点，过坐标原点O的直线
与抛物线交于M、N两点.分别过点C、D
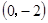作平行于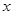
轴的直线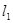
、
.（1）求抛物线对应的二次函数的解析式；（2）求证:以ON为直径的圆与直线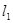相切；（3）求线段MN的长（用
表示），并证明M、N两点到直线的距离之和等于线段MN的长.
四棱锥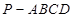
如图放置，
,
，
，
为等边三角形．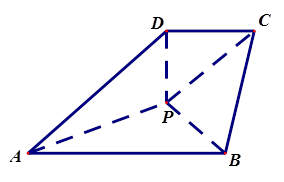
（Ⅰ）证明：
；
（Ⅱ）求二面角
的平面角的余弦值．
在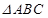
中，角
的对边分别为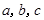
，已知
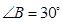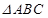,的面积为
．
（Ⅰ）当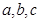
成等差数列时，求
；
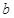（Ⅱ）求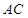
边上的中线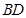
的最小值．
(本小题满分14分)已知函数f(x)＝(1＋x)lnx.
(1)求函数f(x)在x＝1处的切线方程；
(2)设g(x)＝
，对任意x∈(0，1)，都有g(x)＜－2，求实数a的取值范围；
(本小题满分13分)已知椭圆C:
(a＞b＞0)的两个焦点分别为F1(－
，0)、F2(，0).点M(1，0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程；
(2)过点M(1，0)的直线l与椭圆C相交于A、B两点，设点N(3，2)，记直线AN、BN的斜率分别为k1、k2，求证k1＋k2为定值.
(本小题满分12分)已知等差数列{an}的前n项和为Sn＝n2＋pn＋q(p，q∈R)，且a2，a3，a5成等比数列
(1)求p，q的值；
(2)若数列{bn}满足an＋log2n＝log2bn，求数列{bn}的前n项和Tn.