假设宇宙中存在一些离其它恒星较远的、由质量相等的四颗星组成的四星系统，设其它星体对它们的引力作用可忽略。已知稳定的四星系统存在两种基本构成形式，一种形式是三颗星位于等边三角形的三个顶点上，第四颗位于其中心，顶点上的三颗星沿外接于等边三角形的圆形轨道运行；另一种形式是四颗星位于正方形的四个顶点上，围绕正方形的中心做圆轨道运行。设所有星体的质量均相等，等边三角形边长和正方形边长相等，试求出这两种情况下四星系统的运动周期T1和T2之比。
物块以V0=4米/秒的初速度从底端匀减速滑上光滑的斜面，途经A、B两点，已知在A点时的速度是B点时的速度的2倍，由B点再经0.5秒物块滑到斜面顶点C速度变为零，A、B相距0.75米，求：
(1)物体由A运动到B的时间？（2）物体的加速度？(3)斜面的长度？
用绳AC和BC吊起一重物处于静止状态，如图所示． AC绳与竖直方向夹角370，BC绳与竖直方向夹角为530，g取10 m/s2，sin370=0.6，sin530=0.8。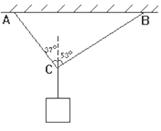
求：（1）当所挂重物质量为4kg时，两绳子所受拉力多大？
（2）若AC能承受的最大拉力为80 N，BC能承受的最大拉力为90 N，为使两绳不断，则所挂物体质量不能超过多少？
如图所示，水平面有一质量m=5kg的物体，受到F1=15N和F2=8N的水平力作用而保持静止。已知物体与水平面间的动摩擦因数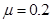
，设最大静摩擦力等于滑动摩擦力，求：
（1）物体所受的摩擦力的大小与方向；
（2）若只将F1撤去，物体受到的摩擦力的大小和方向；
（3）若只将F2撤去，则物体物体受到的摩擦力的大小和方向。
一辆汽车做匀减速直线运动，初速度为40m/s，加速度大小为8m/s2，求：
（1）汽车从开始减速起2s内的位移；
（2）汽车从开始减速起6s内的位移是多少？
水滴从屋檐上由静止自由下落，经过高度为1.8m的窗户，历时0.2s，若不计空气阻力，g取10m/s2，求屋檐离窗顶的高度和水滴落到窗底的速度大小。