如图所示，一质量为1 kg的小球套在一根固定的直杆上，直杆与水平面夹角θ为30°。现小球在F="20" N的竖直向上的拉力作用下，从A点静止出发向上运动，已知杆与球间的动摩擦因数μ为
。试求：
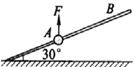
（1）小球运动的加速度a1；
（2）若F作用1．2s后撤去，小球上滑过程中距A点最大距离sm；
（3）若从撤去力F开始计时，小球经多长时间将经过距A点上方为2．25 m的B点。
(15分)在游乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论。如图所示，他们将选手简化为质量m=60kg的质点， 选手抓住绳由静止开始摆动，此时绳与竖直方向夹角
=，绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取重力加速度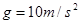
， 
，
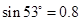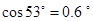
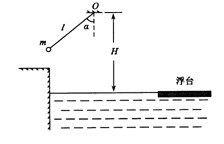
（1）求选手摆到最低点时对绳拉力的大小F；
（2）若绳长l="2m," 选手摆到最高点时松手落入手中。设水对选手的平均浮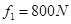力
，平均阻力
，求选手落入水中的深度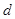
；
（3）若选手摆到最低点时松手， 小明认为绳越长，在浮台上的落点距岸边越远；小阳认为绳越短，落点距岸边越远，请通过推算说明你的观点。
在某些恒星内，3个α粒子可以结合成一个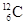
核，已知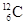核的质量为1.99502×10-26kg, α粒子的质量为6.64672×10-27kg，真空中的光速c=3×108m/s，计算这个反应中所释放的核能（结果保留一位有效数字）。
(14分)如图所示，弧形轨道的下端与半径为R的圆轨道平滑连接。现在使小球从弧形轨道上端距地面2R的A点由静止滑下，进人圆轨道后沿圆轨道运动，轨道摩擦不计。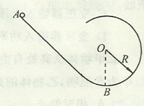
试求：
(1)小球到达圆轨道最低点B时的速度大小；
(2)小球在最低点B时对轨道的压力大小；
(3)小球在某高处脱离圆轨道后能到达的最大高度。
(14分)如图所示，在一宽度D="16" cm的区域内，同时存在相互垂直的匀强磁场B和匀强电场E，电场的方向竖直向上，磁场的方向垂直向外。一束带电粒子以速度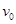
同时垂直电场和磁场的方向射入时，恰不改变运动方向。若粒子射入时只有电场，可测得粒子穿过电场时沿竖直方向向上偏移6．4 cm；若粒子射人时只有磁场，则粒子束离开磁场时偏离原方向的距离是多少?不计粒子的重力。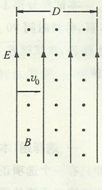
(10分)如图所示，两根平行且光滑的金属轨道固定在斜面上，斜面与水平面之间的夹角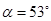
，轨道上端接一只阻值为R=0.4
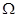的电阻器，在导轨间存在垂直于导轨平面的匀强磁场，磁场的磁感应强度B=0．5 T，两轨道之间的距离为L=40cm，且轨道足够长，电阻不计。现将一质量为m="3" g，有效电阻为r=1.0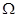的金属杆ab放在轨道上，且与两轨道垂直，然后由静止释放，求：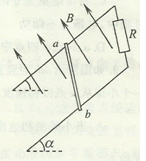
(1)金属杆ab下滑过程中可达到的最大速率；
(2)金属杆ab达到最大速率以后，电阻器R每秒内产生的电热。