如图,在7×7的正方形网格中有一个△ABC 
(1)画出以点B为旋转中心,将△ABC按顺时针方向旋转90°后的图形。
(2)画BC边上的高。
(3)求△ABC的面积(画图不写作法)
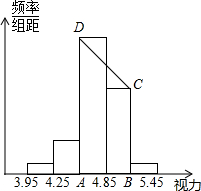
青少年视力水平的下降已经引起全社会的关注,某校为了了解初中毕业年级500名学生的视力情况,从中抽查了一部分学生视力,通过数据处理,得到如下频率分布表和频率分布直方图:
请你根据给出的图表回答:
(1)填写频率分布表中未完成部分的数据,
(2)在这个问题中,总体是_________ ,样本容量是__________ .
(3)在频率分布直方图中梯形ABCD的面积是____________ .
(4)请你用样本估计总体,可以得到哪些信息 .(写一条即可)
___________________________________________________。
| 分组 |
频数 |
频率 |
| 3.95—4.25 |
2 |
0.04 |
| 4.25—4.55 |
6 |
0.12 |
| 4.55—4.85 |
25 |
|
| 4.85—5.15 |
||
| 5.15—5.45 |
2 |
0.04 |
| 合计 |
要了解某地区八年级学生的身高情况从中随机抽取150名学生个身高作为一个样本,身高均在140cm~175cm之间(取整数厘米),整理后分成7组,会制频率分布直方图(不完整).根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)抽取的样本中,学生的身高的中位数在哪个小组;
(3)该地区共有3 000名八年级学生,估计其中身高不低于161cm的人数.
网瘾低龄化问题已引起社会各界的高度关注.有关部门在全国范围内对12~35岁的网瘾人群进行了抽样调查.下图是用来表示在调查的样本中不同年龄段的网瘾人数的,其中30~35岁的网瘾人数占样本总人数的20%.
(1)被抽样调查的样本总人数为___________ 人;
(2)请把统计图中缺失的数据、图形补充完整;
(3)据报道,目前我国12~35岁网瘾人数约为200万人,那么其中12~17岁的网瘾人数约有多少人?
某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示).
(1)这50名学生在这一天课外阅读所用时间的众数是多少?
(2)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(3)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人? 
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图.请根据图中信息解决下列问题:
(1)本次抽查活动中共抽查了多少名学生?
(2)请估算该城区视力不低于4.8的学生所占的比例,用扇形统计图在图中表示出来;
(3)假设该城区八年级共有4000名学生,请估计这些学生中视力低于4.8的学生约有多少人?