某冰箱厂为响应国家“家电下乡”号召,计划生产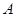 、
、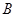 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
| 型号 |
A型 |
B型 |
| 成本(元/台) |
2200 |
2600 |
| 售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
(本题满分12 分)
分)
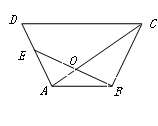
如图,梯形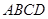 中,
中,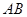 ∥
∥ ,
,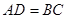 ,点
,点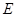 在边
在边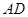 上,
上, 与
与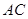 相交于点
相交于点 ,且
,且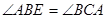 .
.
求证:(1)
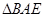 ∽
∽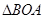 ;
; (2)
 .
.
小楠家附近的公路上通行车辆限速为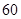 千米/小时.小楠家住在距离公路
千米/小时.小楠家住在距离公路 米的居民楼(
米的居民楼( 如图8中的P点处),在他家前有一道路指示牌
如图8中的P点处),在他家前有一道路指示牌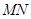 正好挡住公路上的
正好挡住公路上的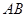 段(即点
段(即点 和点
和点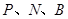 分别在一直
分别在一直 线上),已知
线上),已知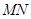 ∥
∥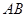 ,
, 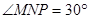 ,
, ,小楠看见一辆卡车通过
,小楠看见一辆卡车通过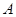 处,
处, 秒后他在
秒后他在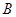 处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据:
处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据: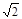 ≈1.41,
≈1.41,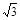 ≈1.73)
≈1.73)
如图,在 中,点
中,点 在边
在边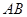 上,点
上,点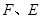 在边
在边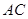 上,且
上,且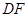 ∥
∥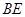 ,
, .
.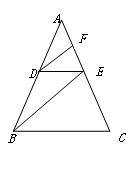
(1)求证:
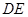 ∥
∥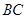 ;
;(2)如果
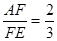 ,
,
 ,求
,求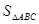 的值.
的值.
如图,□ 中,
中, ∥
∥ ,
, ∥
∥ ,点
,点 是
是 的中点,
的中点, 和
和 相交于点
相交于点 .
.
(1)求
 的值;
的值; (2)如果
(2)如果 ,
, ,请用
,请用 、
、 表示
表示
(本题满分14分,其中第(1)、(2)小题各4分,第(3)小题6分)已知:如图,在平面直角坐标系xOy中,二次函数 的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
(1)求这个二次函数的解析式和它的对称轴;
(2)求证:∠ABO=∠CBO;
(3)如果点P在直线AB上,且△POB
与△BCD相似,求点P的坐标.