(本小题满分12分)最近,李师傅一家三口就如何将手中的10万元钱进行投资理财,提出了三种方案.
第一种方案:李师傅的儿子认为:根据股市收益大的特点,应该将10万元全部用来买股票.据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为0.5.
第二种方案:李师傅认为:现在股市风险大,基金风险较小,应将10万元全部用来买基金.据分析预测:投资基金一年后可能获利20%,可能损失10%,也可能不赔不赚,且这三种情况发生的概率分别为
第三种方案:李师傅的妻子认为:投资股市、基金均有风险,应将10万元全部存入银行一年,现在存款年利率为4%,存款利息利率为5%.
针对以上三种投资方案,请你为李师傅家选择一种合理的理财方案,并说明理由.
(本小题满分7分)选修4-5:不等式选讲
已知 (
( ,
,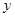 ,
, ).
).
(1)求 的最小值;
的最小值;
(2)若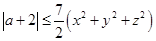 对满足条件的一切实数
对满足条件的一切实数 ,
,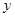 ,
, 恒成立,求实数
恒成立,求实数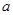 的取值范围.
的取值范围.
(本小题满分7分)选修4-4:极坐标与参数方程
在平面直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线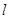 的极坐标方程为
的极坐标方程为 (
(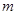 为常数),圆
为常数),圆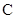 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)求直线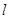 的直角坐标方程和圆
的直角坐标方程和圆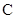 的普通方程;
的普通方程;
(2)若圆心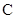 关于直线
关于直线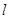 的对称点亦在圆上,求实数
的对称点亦在圆上,求实数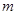 的值.
的值.
(本小题满分7分)选修4-2:矩阵与变换
已知线性变换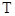 把点
把点 变成了点
变成了点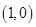 ,把点
,把点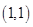 变成了点
变成了点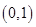 .
.
(1)求变换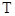 所对应的矩阵
所对应的矩阵 ;
;
(2)求直线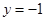 在变换
在变换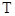 的作用下所得到的直线方程.
的作用下所得到的直线方程.
(本小题满分14分)已知函数 (
( ).
).
(1)当 时,求函数
时,求函数 的图象在点
的图象在点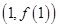 处的切线方程;
处的切线方程;
(2)设 ,求证:当
,求证:当 时,
时, ;
;
(3)若函数 恰有两个零点
恰有两个零点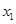 ,
, (
( ),求实数
),求实数 的取值范围.
的取值范围.
(本小题满分13分)如图,在四棱锥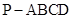 中,侧棱
中,侧棱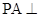 底面
底面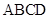 ,
,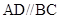 ,
, ,
,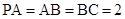 ,
, ,
, 是棱
是棱 中点.
中点.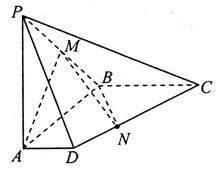
(1)求证: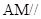 平面
平面 ;
;
(2)设点 是线段
是线段 上一动点,且
上一动点,且 ,当直线
,当直线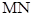 与平面
与平面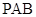 所成的角最大时,求
所成的角最大时,求 的值.
的值.