小红和小新两人解方程组, ,
,
小红一边做作业,一边看电视,不小心把a给看错了,从而得到方程组的解为 ,
,
小新一边做作业,一边吃零食,一走眼把b看错了,从而得到方程组的解为 ,
,
若按正确的a、b计算,原方程组的解是什么?
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.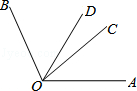
在图的正方形网格中有一个三角形OAB,请你在网格中分别按下列要求画出图形
①画出△OAB向左平移3个单位后的三角形;
②画出△OAB绕点O旋转180°后的三角形;
③画出△OAB沿y轴翻折后的图形.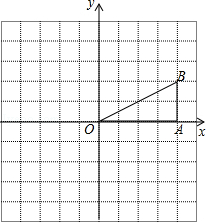
(1)由大小相同的小立方块搭成的几何体如下图,请在下图的方格中画出该几何体的俯视图和左视图.
(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
先化简,再求值(3ab﹣2b)+[3a﹣(5ab﹣12b﹣2a)],其中a+2b=﹣5,ab=﹣3.
解方程
(1)4x﹣3(5﹣x)=6
(2) ﹣
﹣ =1.
=1.