一质点沿直线ox方向作加速运动,它离开o点的距离x随时间变化的关系为x=5+2t3(m),它的速度随时间变化的关系为v=6t2(m/s)。求:
(1)该质点在前2s的位移大小
(2)质点在第3s内的平均速度的大小。
.(10分)如图所示,MN是匀强磁场的左边界(右边范围很大),磁场方向垂直纸面向里,在磁场中有一粒子源P,它可以不断地沿垂直于磁场方向发射出速度为v、电荷为+q、质量为m的粒子(不计粒子重力).已知匀强磁场的磁感应强度为B,P到MN的垂直距离恰好等于粒子在磁场中运动的轨道半径.求在边界MN上可以有粒子射出的范围.
用电流传感器和电压传感器等可测干电池的电动势和内电阻.改变电路的外电阻,通过电压传感器和电流传感器测量不同工作状态的端电压和电流,输入计算机,自动生成U-I图线,由图线得出电动势和内电阻.
(1)记录数据后,打开“坐标绘图”界面,设x轴为“I”,y轴为“U”,点击直接拟合,就可以画出U-I图象,得实验结果如图甲所示.根据图线显示,拟合直线方程为:________,测得干电池的电动势为________V,干电池的内电阻为________Ω.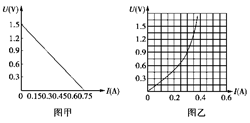
(2)现有一小灯泡,其U-I特性曲线如图乙所示,若将此小灯泡接在上述干电池两端,小灯泡的实际功率是多少?(简要写出求解过程;若需作图,可直接画在方格图中).
如图所示,光滑匀质圆球的直径为d=40 cm,质量为M=20 kg,悬线长L=30 cm,正方形物块A的厚度b=10 cm,质量为m=2 kg,物块A与墙之间的动摩擦因数μ=0.2.现将物块A轻放于球和墙之间后放手,取g=10 m/s2.求:
(1)墙对A的摩擦力为多大?
(2)如果在物块A上施加一个与墙平行的外力F,使A在未脱离圆球前贴着墙沿水平方向做加速度a=5 m/s2的匀加速直线运动,那么这个外力F的大小和方向如何?
一个滑板运动员,滑板和人总质量为50kg,以12m/s的速度从一斜坡底端滑上斜坡,当速度减为零时,又从斜坡上下滑至底端,已知斜坡的倾角为300,运动员上滑时用时为2s,设滑板受的阻力大小恒定不变,(g=10m/s2)求:
(1)滑板受到的阻力大小;
(2)运动员匀加速下滑至底端时所需的时间。
如图所示,质量为30kg的小孩坐在质量为10kg的雪橇上,大人用与水平方向成37º斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速直线运动,求:
(1)水平地面对雪橇的支持力的大小
(2)雪橇与水平地面的动摩擦因数
(已知sin37º="0.6" cos37º=0.8,g="10" m/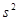 )
)