正负电子对撞机的最后部分的简化示意图如图甲所示(俯视图),位于水平面内的粗实线所示的圆环形真空管道是正、负电子做圆运动的“容器”,经过加速器加速后的正、负电子被分别引入该管道时,具有相等的速率v,它们沿着管道向相反的方向运动.在管道内控制它们转弯的是一系列圆形电磁铁,即图中的A1、A2、A3……An共有n个,均匀分布在整个圆环上,每个电磁铁内的磁场都是磁感应强度相同的匀强磁场,并且方向竖直向下,磁场区域的直径为d,改变电磁铁内电流的大小,就可改变磁场的磁感应强度,从而改变电子偏转的角度.经过精确的调整,首先实现电子在环形管道中沿图甲中粗虚线所示的轨迹运动,这时电子经过每个电磁场区域时射入点和射出点都是电磁场区域的同一条直径的两端,如图乙所示.这就为进一步实现正、负电子的对撞作好了准备.
(1)试确定正、负电子在管道内各是沿什么方向旋转的;
(2)已知正、负电子的质量都是m,所带电荷都是元电荷e,重力可不计,求电磁铁内匀强磁场的磁感应强度B的大小.
如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能。
如图所示,竖直放置的半圆形绝缘光滑轨道半径R=40cm,下端与绝缘光滑的水平面平滑连接,整个装置处于方向竖直向下,大小为E=1×103V/m的匀强电场中,一质量为m=10g、带电量为q=+1×10-4C的小物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,取g=10m/s2,试求:
(1)小物块从C点抛出后落地点与B点间的水平距离;
(2)v0的大小和过B点时轨道对小物块的支持力大小;
一灵敏电流计,允许通过的最大电流(满刻度电流)为Ig=50μA,表头电阻Rg=1kΩ
(1)若改装成量程为Im=1mA的电流表,应该串联还是并联一个电阻? 新表内阻为多少?
(2)若将改装后的电流表再改装成量程为Um=10V的电压表,应该再串联还是并联一个多大的电阻?
如图所示的匀强电场中,有a、b、c三点,ab间距离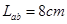 ,bc间距离
,bc间距离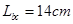 ,其中ab沿电场方向,bc和电场方向成60°角.一个所带电量
,其中ab沿电场方向,bc和电场方向成60°角.一个所带电量 的负电荷从a点移到b点克服电场力做功
的负电荷从a点移到b点克服电场力做功 .求:
.求:
(1)匀强电场的电场强度;
(2)电荷从b点移到c点,电场力所做的功;
(3)a、c两点间的电势差.
一台小型电动机在3V电压下工作,通过它的电流是0.2A,用此电动机提升物重4N的物体,在30秒内可以使该物体匀速提升3m,除电动机线圈生热之外不计其它的能量损失,求
(1)电动机的输入电功率。
(2)在提升重物的30秒内,电动机线圈所产生的热量。
(3)线圈的电阻。