选修4-4:坐标系与参数方程
已知曲线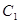 的极坐标方程是
的极坐标方程是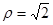 ,曲线
,曲线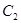 的参数方程是
的参数方程是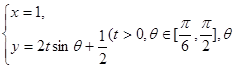 是参数).
是参数).
(1)写出曲线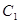 的直角坐标方程和曲线
的直角坐标方程和曲线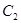 的普通方程;
的普通方程;
(2)求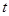 的取值范围,使得
的取值范围,使得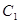 ,
,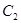 没有公共点.
没有公共点.
一个包装箱内有6件产品,其中4件正品,2件次品.现随机抽出两件产品,
(1)求恰好有一件次品的概率.
(2)求都是正品的概率.
(3)求抽到次品的概率.
设计程序框图计算12+22+32+…+10002,并写出程序.
某人群中各种血型的人所占的比例如下:
| 血型 |
A |
B |
AB |
O |
| 该血型的人所占比例(%) |
28 |
29 |
8 |
35 |
已知同种血型的人可以输血,O型血可以输给任何一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
已知不等式xy≤ax2+2y2,若对任意x∈[1,2],且y∈[2,3],该不等式恒成立,求实数a的取值范围
已知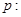
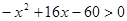 ,
,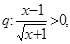
 关于
关于 的不等式
的不等式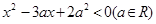 ,
,
若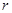 是
是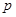 的必要不充分条件,且
的必要不充分条件,且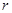 是
是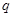 的充分不必要条件,试求
的充分不必要条件,试求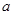 的取值范围.
的取值范围.