如图所示,ε1=3V,r1=0.5Ω,R1=R2=5.5Ω,平行板电容器的两板距离d=1cm,当电键K接通时极板中的一个质量m=4×10-3g,电量为q=1.0×10-7C的带电微粒恰好处于静止状态。求:
(1)K断开后,微粒向什么方向运动,加速度多大?
(2)若电容为1000pF,K断开后,有多少电量的电荷流过R2?
如图所示,两带电平行板A、B间的电场为匀强电场,场强E=8.0×102V/m,两板间距d=16cm,板长L=30cm。一带电量q=1.0×10-16C、质量m=1.0×10-24kg的粒子以v0=3×105m/s的速度沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子的重力,求: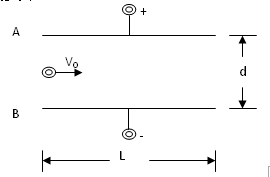
粒子待何种电荷?在电场中运动时间为多久?
粒子废除电场时的偏转角的正弦值为多大
如图所示。光滑水平面上的木板C的质量mC=2kg、长l=2m,它的BA两端各有块挡板。木板的正中央并列放着两个可以视为质点的滑块A和B,它们的质量mA=1kg、mB=4kg,A、B之间夹有少许炸药。引爆炸药,A、B沿同一直线向两侧分开,运动到两端的挡板时与板粘贴在一起。A、B与木板C之间的摩擦不计。引爆时间及A、B跟挡板碰撞的时间也不计。若爆炸后A获得的速度vA=6m/s,试计算: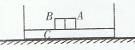
A、B都与挡板粘贴在一起以后,木板C的速度。
从引爆炸药到A、B 都与挡板粘贴在一起的时间差。
一列简谐横波的波速v=40cm/s,在某一时刻的波形如图所示,在这一时刻质点A 振动的速度方向沿y轴正方向。求: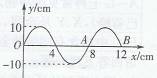
这列波的频率、周期和传播方向。
从这一时刻起在0. 5s 内质点B运动的路程和位移。
画出再经过0.75s 时的波形图。
如图所示,一定质量的气体温度保持不变,最初,U形管两臂中的水银相齐,烧瓶中气体体积为800ml;现用注射器向烧瓶中注入200ml水,稳定后两臂中水银面的高度差为25. 3cm;已知76cm高的水银柱产生的压强约为l.0×105Pa,不计U形管中气体的体积。求:
大气压强。 .
当U形管两边懒面的高度差为45.6cm( 左高右低)时,烧瓶内气体的体积。
如图所示,在平面直角坐标系xOy 中,在y>0 的区域内存在垂直于纸面向外的匀强磁场,磁感应强度的大小为B在y<0 的区域内存在另一未知的匀强磁场。已知P点的坐标(-d,0),Q点的坐标(0,-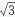 d),在原点O和Q处分别固定一个垂直于y轴的较小的弹性挡板,当粒子与挡板碰撞后在平行于挡板的方向上速度不变,在垂直于挡板的方向上速度大小不变、方向与原方向相反。一质量为m、电荷量为q的带正电粒子(重力不计)从P点沿垂直于x轴的方向进入第二象限内,在x轴上方运动半周后进入x轴下方,若粒子又能返回P点,试求:
d),在原点O和Q处分别固定一个垂直于y轴的较小的弹性挡板,当粒子与挡板碰撞后在平行于挡板的方向上速度不变,在垂直于挡板的方向上速度大小不变、方向与原方向相反。一质量为m、电荷量为q的带正电粒子(重力不计)从P点沿垂直于x轴的方向进入第二象限内,在x轴上方运动半周后进入x轴下方,若粒子又能返回P点,试求:
y<0 区域内的磁场的磁感应强度的大小和方向。
若不计粒子与挡板的碰撞时间,粒子从P 点出发至返回P 点的时间。