我们知道：若x2=9，则x=3或x=－3．
因此，小南在解方程x2+2x－8=0时，采用了以下的方法：
解：移项，得x2+2x=8：
两边都加上l，得x2+2x+1=8+1，所以(x+1) 2=9；
则x+1=3或x+1=－3：
所以x=2或x=－4．
小南的这种解方程方法，在数学上称之为配方法．请用配方法解方程x2－4x－5=0．
如图，平面直角坐标系中，过点C（28，28）分别作x轴、y轴的垂线，垂足分别为B、A，一次函数y=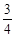
x+3的图像分别与x轴和CB交于点D、E，点P 是DE中点，连接AP.
（1）求证：△ADO≌△AEC；
（2）求AP的长．
如图，在Rt△ABC中，∠ACB=90º，AC=3cm，BC=4cm．动点P从点B出发，以每秒1cm的速度沿射线BA运动，求出点P运动所有的时间t，使得△PBC为等腰三角形.
如图，一次函数y=（m－1）x+3的图像与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB面积为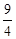
.
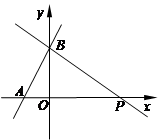
（1）求m的值及点A的坐标；
（2）过点B作直线BP与x轴的正半轴相交于点P，且OP=2OA，求直线BP的函数表达式 ．
如图，已知点P在∠AOB内部，请你利用直尺（没有刻度）和圆规在∠AOB的角平分线上求作一点Q，使得PQ⊥OB.（不要求写作法，但要保留作图痕迹）
学校为了开阔学生的视野，积极组织学生参加课外读书活动．“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：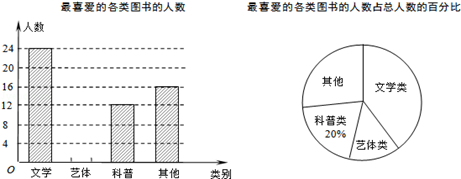
（1）求被调查的学生人数；
（2）补全条形统计图；
（3）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？