如图，正方形网格中，小格的顶点叫做格点，连接任意两个格点的线段叫做格点线段。
(1)如图1，格点线段AB、CD，请添加一条格点线段EF，使它们构成轴对称图形；
(2)如图2，格点线段AB和格点C，在网格中找一格点D，使格点A、B、C、D四点构成中心对称图形；
(3)在(2)的条件下，如果每一小正方形边长为1，那么四边形ABCD的面积S为_________．
(请直接填写)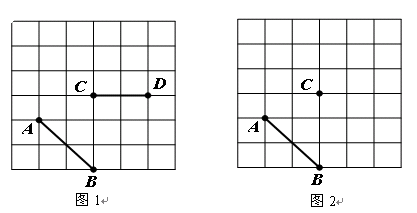
解方程：
（1）
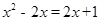=0
（2）
．
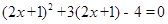如图，在平面直角坐标系中，O为坐标原点．△ABC的边BC在x轴上，A、C两点的坐标分别为A（0，m）、C（n，0），B（﹣5，0），且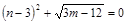
，点P从B出发，以每秒2个单位的速度沿射线BO匀速运动，设点P运动时间为t秒．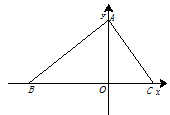
（1）求A、C两点的坐标；
（2）连接PA，用含t的代数式表示△POA的面积；
（3）当P在线段BO上运动时，是否存在一点P，使△PAC是等腰三角形？若存在，请写出满足条件的所有P点的坐标并求t的值；若不存在，请说明理由．
阅读材料：矩形的四个内角都是直角，矩形的对边平行且相等．利用阅读材料解决下列问题：如图，在矩形ABCD中，AB=6，BC=8，将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的F处．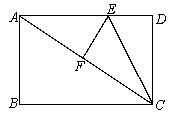
（1）求EF的长；
（2）求梯形ABCE的面积．
如图，已知：点P（2m-1，6m-5）在第一象限角平分线OC上，∠BPA=90°，角两边与x轴、y轴分别交于A点、B点．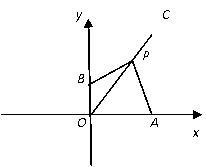
（1）求点P的坐标
（2）若点A（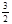
，0），求点B的坐标．
如图，在平面直角坐标系xOy中，点A（0，8），点B（6，8）．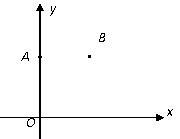
（1）只用直尺（没有刻度）和圆规，求作一个点P，使点P同时满足下列两个条件（要求保留作图痕迹，不必写出作法）：
①点P到A、B两点的距离相等；
②点P到∠xOy的两边距离相等．
（2）若在x轴上有点M，则能使△ABM的周长最短的点M的坐标为 ．