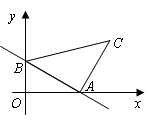
解方程:16=4x
牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价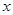 (元/件) (元/件) |
… |
20 |
30 |
40 |
50 |
60 |
… |
每天销售量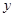 (件) (件) |
… |
500 |
400 |
300 |
200 |
100 |
… |
(1)把上表中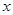 、
、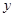 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想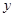 与
与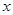 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?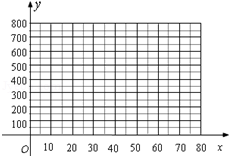
某中学举行数学知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图.根据图中所给出的信息解答下列问题: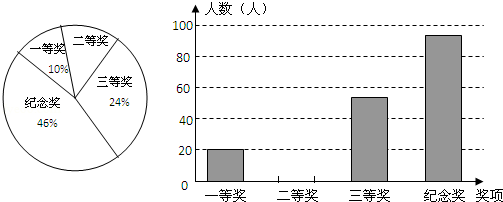
(1)二等奖所占的比例是多少?
(2)这次数学知识竞赛获得二等奖的人数是多少?
(3)请将条形统计图补充完整;
(4)若给所有参赛学生每人发一张卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出的卡片上是写有一等奖学生名字的概率.
如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:用尺规作图,保留痕迹,不写作法与证明).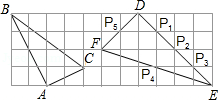
我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
如图,一次函数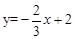 的图象分别与
的图象分别与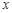 轴、
轴、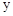 轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.
轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.求过B、C两点直线的解析式.