如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是APB上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．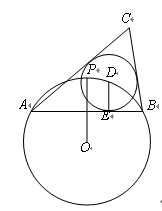
（1）求弦AB的长；
（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；
（3）记△ABC的面积为S，若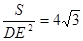
，求△ABC的周长.
如图，抛物线y=-x2+bx+c与直线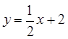
交于C、D两点，其中点C在y轴上，点D的坐标为（3，
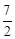）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F，设点P的横坐标为m。
（1）求抛物线的解析式；
（2）当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由．
（3）若点P在CD上方，则四边形PCOD的面积最大时，求点P的坐标。
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．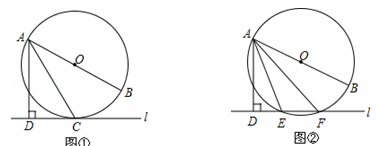
（1）如图①，当直线l与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．
在△ABC中，AB=AC，∠BAC=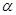
（
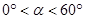），将线段BC绕点B逆时针旋转60°得到线段BD。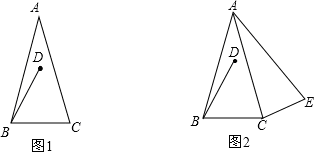
（1）如图1，直接写出∠ABD的大小（用含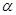的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求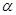的值。
某校数学兴趣小组要测量天塔CD的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB=112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0．73，结果保留整数）．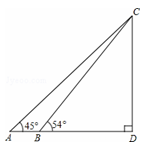
某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：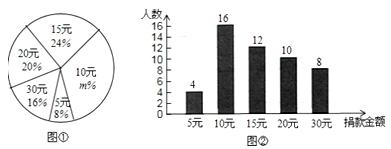
（1）本次接受随机抽样调查的学生人数为，图①中m的值是；
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．