某矿井的升降机由井底从静止开始做匀加速直线运动，经过5s速度达到5m/s，又匀速上升了30s，最后8s做匀减速运动停在井口，求矿井的深度。
如图所示，小车A、B的质量均为m，小车B静止于水平轨道上，其左端固定一根轻弹簧，小车A从高出水平轨道h处由静止开始沿曲轨道滑下，在水平轨道上与小车B发生相互作用．轨道是光滑的．求：
（1）A车沿曲轨道刚滑到水平轨道时的速度大小v0；
（2）弹簧的弹性势能最大时A车的速度v和弹簧的弹性势能Ep 。
天然放射性铀（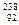
U）发生衰变后产生钍（
Th）和另一种原子核。
（1）请写出衰变方程；
（2）若衰变前铀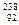（U）核的速度为v，衰变产生的钍（Th）核速度为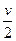
，且与铀核速度方向相同，求产生的另一种新核的速度。
分别用λ和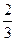
λ的单色光照射同一金属，发出的光电子的最大初动能之比为1∶2，以h表示普朗克常量，c表示真空中的光速，则此金属板的逸出功是多大？
（附加题）已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。
游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来（如图甲）。我们可以把它抽象成图乙所示的由曲面轨道和圆轨道平滑连接的模型（不计摩擦和空气阻力）。若质量为m的小球从曲面轨道上的P点由静止开始下滑，并且可以顺利通过半径为R的圆轨道的最高点A。已知P点与B点的高度差h=3R，求：
（1）小球通过最低点B时速度有多大？
（2）小球通过B点时受到圆轨道支持力有多大？
（3）若小球在运动中需要考虑摩擦和空气阻力，当小球从P点由静止开始下滑，且刚好通过最高点A，则小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功为多少？