如图所示,电源的电动势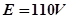 ,电阻
,电阻 ,电动机绕组的电阻
,电动机绕组的电阻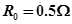 ,电键S1始终闭合。当电键S2断开时,电阻R1的电功率是525W;当电键S2闭合时,电阻R1的电功率是336W,求
,电键S1始终闭合。当电键S2断开时,电阻R1的电功率是525W;当电键S2闭合时,电阻R1的电功率是336W,求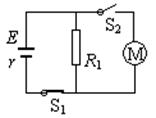
(1)电源的内电阻;
(2)当电键S2闭合时流过电源的电流和电动机的输出功率。
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为a的正方形(不计电子所受重力).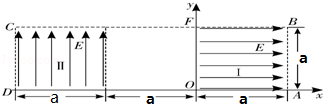
(1)在该区域AB边的中点处由静止释放电子,求电子 离开ABCD区域的位置.
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置.
(3)若将左侧电场Ⅱ整体水平向右移动 (n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场Ⅰ区域内由静止释放电子的所有位置.
(n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场Ⅰ区域内由静止释放电子的所有位置.
如图所示,R为电阻箱,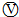 为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求:
为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为U1=4V;当电阻箱读数为R2=5Ω时,电压表读数为U2=5V.求: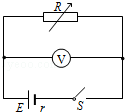
(1)电源的电动势E和内阻r.
(2)当电阻箱R读数为多少时,电源的输出功率最大?最大值Pm为多少?
如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=10kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求:
(1)工件与皮带间的动摩擦因数;
(2)电动机由于传送工件多消耗的电能.
如图所示,A和B是两个相同的带电小球,可视为质点,质量均为m,电荷量均为q,A固定在绝缘地面上,B放在它的正上方很远距离的一块绝缘板上,现手持绝缘板使B从静止起以恒定的加速度a(a<g)竖直下落h时,B与绝缘板脱离.静电力常量为k,求:
(1)B刚脱离绝缘板时的动能.
(2)B在脱离绝缘板前的运动过程中,电场力和板的支持力对B做功的代数和W.
(3)B脱离绝缘板时离A的高度H.
用同种材料制成倾角30°的斜面和长水平面,斜面长2.4m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t﹣v0图象,如图所示,求:
(1)小物块与该种材料间的动摩擦因数为多少?
(2)某同学认为,若小物块初速度为4m/s,则根据图象中t与v0成正比推导,可知小物块运动时间为1.6s.以上说法是否正确?若不正确,说明理由并解出你认为正确的结果.