在平面直角坐标中,直线 (
(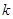 为常数且
为常数且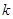 ≠0),分别交
≠0),分别交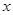 轴,
轴, 轴于点
轴于点 、
、 、⊙
、⊙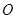 的半径为
的半径为 个单位长度,如图,若点
个单位长度,如图,若点 在
在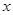 轴正半轴上,点
轴正半轴上,点 在
在 轴的正半轴上,且
轴的正半轴上,且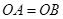 。
。
(1)求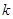 的值。
的值。
(2)若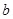 =4,点P为直线
=4,点P为直线 上的一个动点过点
上的一个动点过点 作⊙
作⊙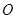 的切线
的切线 、
、 切点分别为
切点分别为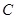 、
、 。当
。当 ⊥
⊥ 时,求点
时,求点 的坐标。
的坐标。
某工厂甲、乙两名工人参加操作技能培训.现分别从他们若干次测试成绩中随机抽取5次,记录如下:
| 次数 |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
平均数 |
中位数 |
|
| 甲 |
87 |
91 |
94 |
90 |
88 |
|||
| 乙 |
91 |
89 |
92 |
86 |
92 |
(1)请你计算两组数据的平均数、中位数,并把求得的结果填入表格中;
(2)分别计算甲、乙两名工人五次测试成绩的方差;
(3)现要从中选派一人参加操作技能比赛,你认为选派哪名工人参加合适?请说明理由.
已知关于x的方程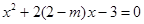 ,
,
(1)若x=1是此方程的一根,求m的值及方程的另一根;
(2)证明:无论m取什么实数值,此方程总有实数根.
(1)解方程: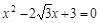
(2)计算: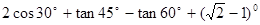
如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.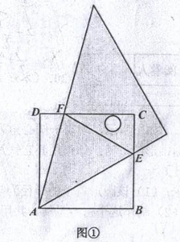
(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F.求证:EF=BE+DF;
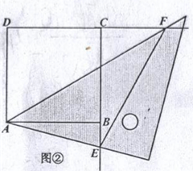
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的边CB、DC交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明;
(3)在图①中,当正方形ABCD的边长为6,EF=5时,BE的长为
(注意:此问占2分)
观察下面方程的解法:x4-13x2+36=0
解:原方程可化为(x2 -4)(x2 -9)=0
∴(x+2)(x -2)(x+3)(x -3)=0
∴x+2=0或x-2=0或x+3=0或x-3=0
∴x1=2,x2= -2,x3=3,x4= -3
你能否求出方程x2 -3|x|+2=0的解?