(9分)如图所示,宽为L=1 m、高为h=7.2 m、质量为M=8 kg、上表面光滑的木板在水平地面上运动,木板与地面间的动摩擦因数为μ=0.2.当木板的速度为v0="3" m/s时,把一原来静止的质量m="2" kg的光滑小铁块(可视为质点)轻轻地放在木板上表面的右端,g取10m/s2.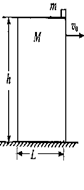
求:(1)小铁块与木板脱离时长木板的速度大小v1;
(2)小铁块刚着地时与木板左端的距离S.
加速性能是汽车的一项重要技术指标。某辆汽车从静止开始加速,经过t="3" s时间速度达到v="15" m/s.在这一加速过程中,汽车的运动可视为匀加速直线运动.求:
(1)该汽车的加速度大小;
(2)6 s内汽车加速运动的位移大小;
(3)第6 s内汽车的平均速率.
如图所示,在水平向右的匀强电场中,有一根长度为 m的绝缘轻细绳,将质量为
m的绝缘轻细绳,将质量为 kg、电荷量
kg、电荷量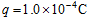 的带正电小球(可看成质点)悬挂在Q点,绳的悬点为
的带正电小球(可看成质点)悬挂在Q点,绳的悬点为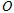 (绳可绕
(绳可绕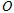 点自由转动),匀强电场的场强大小
点自由转动),匀强电场的场强大小 .现将小球拉到右侧与O等高的P点(细绳伸直),以
.现将小球拉到右侧与O等高的P点(细绳伸直),以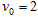 m/s的初速度竖直向下抛出,当小球下摆至最低点
m/s的初速度竖直向下抛出,当小球下摆至最低点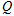 时,匀强电场方向立即变为竖直向上(场强大小不变),当小球运动到圆周的最高点
时,匀强电场方向立即变为竖直向上(场强大小不变),当小球运动到圆周的最高点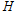 时电场立即消失.求:
时电场立即消失.求: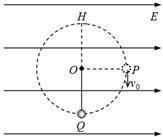
(1)小球第一次下摆至最低点过程中的最大速率;
(2)小球到达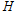 点时的速度大小;
点时的速度大小;
(3)小球第二次到达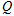 点时细绳对小球的拉力大小.
点时细绳对小球的拉力大小.
(4)电场消失后小球所能达到的最大高度(距离Q点).
如图所示,质量为m、电荷量为e的电子(初速度为0)经加速电压U1加速后,在水平方向沿O1O2垂直进入偏转电场.已知形成偏转电场的平行板电容器的极板长为L(不考虑电场边缘效应),两极板间距为d,O1O2为两极板的中线,P是足够大的荧光屏,且屏与极板右边缘的距离也为L.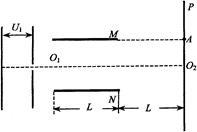
(1)求粒子进入偏转电场的速度v的大小;
(2)若偏转电场两板M、N间加恒定电压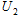 时,电子经过偏转电场后正好打中屏上的A点,A点与极板M在同一水平线上,求
时,电子经过偏转电场后正好打中屏上的A点,A点与极板M在同一水平线上,求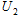 的大小.
的大小.
如图所示,一带电荷量为q=-5×10-3 C,质量为m="0.1" kg的小物块放在一倾角为θ=37°的光滑绝缘斜面上,当整个装置处在一水平向左的匀强电场中时,小物块恰处于静止状态.已知重力加速度g=10m/s2,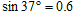 ,
, .
.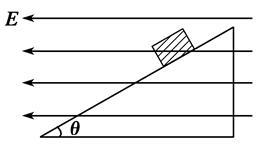
(1)求电场强度E的大小;
(2)某时刻小物块的电荷量突然减少了一半,求物块下滑距离L="1.5" m时的速度大小.
甲、乙两物体,甲的质量为1Kg,乙的质量为0.5Kg,甲从距地45m高处自由落下,1s后乙从距地30m高处自由落下,不计空气阻力.(重力加速度g取10m/s2) 
(1)两物体等高时离地多高?
(2)定量画出两物体间的竖直距离随时间变化的图象.(球落地后立即原地静止,规定甲开始下落时刻为计时起点.)