某学校为改善老师的办公条件，计划购买若干台电脑，现从两个电脑城了解到某品牌同一型号的电脑每台标价都是4000元，但学校集体购买都有一定的优惠．
甲电脑城的优惠方法是：第一台按标价收费，其余每台可优惠15%.则甲电脑城的总收费y1（元）与学校所买电脑的台数x之间的关系式是 ．
乙电脑城的优惠方法是：每台都优惠12%.则乙电脑城的总收费y2（元）与学校所买电脑的台数x之间的关系式是 ．
⑴学校在什么情况下到甲电脑城购买更优惠？
⑵学校在什么情况下到乙电脑城购买更优惠？
解方程：(1) 
－2x－2＝0(2)3
如图，抛物线
与x轴交于点A（—2，0），交y轴于点B（0，
）.直
过点A与y轴交于点C，与抛物线的另一个交点是D.
（1）求抛物线与直线的解析式；
（2）设点P是直线AD下方的抛物线上一动点（不与点A、D重合），过点P作 y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；
（3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为m，点P的横坐标为x，求m与x的函数关系式，并求出m的最大值．
如图①，已知线段AB=8，以AB为直径作半圆O，再以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D。
（1）判断线段AP与PD的大小关系，并说明理由；
（2）连接PC，当∠ACP=600时，求弧AD的长；
（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．
小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元；如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？
如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB．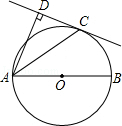
（1）求证：DC为⊙O的切线；
（2）若⊙O的半径为3，AD=4，求AC的长．