网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网两种收费方式,用户可以任选其一:A:计时制:0.05元/分;B:全月制:54元/月(限一部个人住宅电话入网)。此外B种上网方式要加收通信费0.02元/分。
①某用户某月上网的时间为x小时,两种收费方式的费用分别为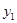 (元)、
(元)、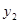 (元),写出
(元),写出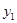 、
、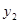 与x之间的函数关系式。
与x之间的函数关系式。
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
如图,AB∥CD,∠A=34°,∠DFB=105º,求∠C的度数.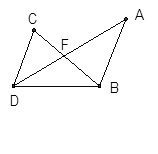
解下列不等式,并把它们的解集在数轴上表示出来。
(1)、 (2)、
(2)、 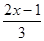



、(1)解方程组 (2)解方程组
(2)解方程组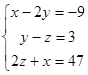
在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:
① ∠PEF的大小是否发生变化?请说明理由;
② 直接写出从开始到停止,线段EF的中点所经过的路线长.

在平面直角坐标系xOy中,抛物线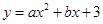 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.