(10分）如图所示，半径为R的四分之一圆弧轨道放在水平面上，且圆弧上端切线竖直，下端与水平面平滑相切。另有一质量为m的小球以速度
冲上圆弧轨道，已知圆弧轨道的质量M=3m，不计摩擦和空气阻力，
求：(1)小球冲出圆弧轨道后能继续上升的最大高度h=?
(2)在小球上升h的过程中圆弧轨道移动的距离S=？
如图所示，线圈L的自感系数为25 mH，电阻为零，电容器C的电容为40 μF，灯泡D的规格是“4 V、2 W”．开关S闭合后，灯泡正常发光，S断开后，LC中产生振荡电流．若从S断开开始计时，求：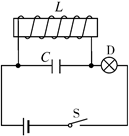
(1)当t＝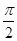
×10－3 s时，电容器的右极板带何种电荷；
(2)当t＝π×10－3 s时，LC回路中的电流．
在真空中传播的波长是20 m的电磁波，进入某一介质中传播时，其传播速度为1×108 m/s，求此电磁波在介质中的波长．
如图所示，一列沿x轴正方向传播的简谐横波，波速大小为0.3 m/s，P点的横坐标为96 cm，从图中状态开始计时，求：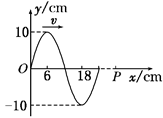
(1)经过多长时间，P质点开始振动，振动时方向如何？
(2)经过多长时间，P质点第一次到达波峰？
(3)以P质点第一次到达波峰开始计时，作出P点的振动图像(至少画出1.5个周期)
一列简谐横波沿x轴正方向传播，t＝0时刻的波形如图所示，介质中质点P、Q分别位于x＝2 m、x＝4 m处．从t＝0时刻开始计时，当t＝15 s时质点Q刚好第4次到达波峰．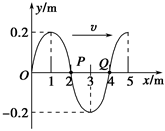
(1)求波速．
(2)写出质点P做简谐运动的表达式(不要求推导过程)．
渔船常利用超声波来探测远处鱼群的方位．已知某超声波频率为1.0×105 Hz，某时刻该超声波在水中传播的波动图像如图所示．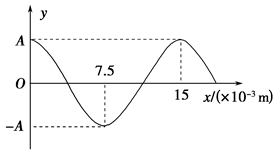
(1)从该时刻开始计时，画出x＝7.5×10－3 m处质点做简谐运动的振动图像(至少一个周期)．
(2)现测得超声波信号从渔船到鱼群往返一次所用时间为4 s，求鱼群与渔船间的距离(忽略船和鱼群的运动)．