写出下列函数的关系式：有一个角是60°的直角三角形的面积S与斜边x的之间的函数关系式．
已知：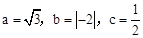
．求代数式：
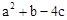的值．
如图，已知抛物线
与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．
（1）求抛物线的解析式及它的对称轴方程；
（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；
（3）试判断△AOC与△COB是否相似？并说明理由；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若不存在，求出符合条件的Q点坐标；若不存在，请说明理由．
如图，在平面直角坐标系xOy中，正比例函数y=kx的图象与反比例函数
的图象有一个交点A（m，2）．
（1）求m的值；
（2）求正比例函数y=kx的解析式；
（3）试判断点B（2，3）是否在正比例函数图象上，并说明理由．
如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．
（1）求DE的长；
（2）求△ADB的面积．
吉首城区某中学组织学生到距学校20km的德夯苗寨参加社会实践活动，一部分学生沿“谷韵绿道”骑自行车先走，半小时后，其余学生沿319国道乘汽车前往，结果他们同时到达（两条道路路程相同），已知汽车速度是自行车速度的2倍，求骑自行车学生的速度．