同学们都知道,在相同的时刻,物高与影长成比例,某班同学要测量学校国旗的旗杆高度,在某一时刻,量得旗杆的影长是8米,而同一时刻,量得某一身高为1.5米的同学的影长为1米,求旗杆的高度是多少?
当x是多少时,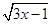 在实数范围内有意义?
在实数范围内有意义?
已知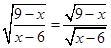 ,且x为偶数,求(1+x)
,且x为偶数,求(1+x)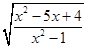 的值.
的值.
化简:
(1)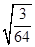 (2)
(2)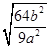 (3)
(3)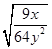 (4)
(4)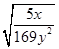
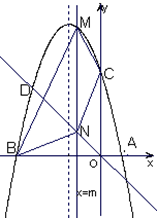
如图,抛物线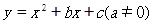 与x轴交于A(1,0)、B(-4,0)两点。
与x轴交于A(1,0)、B(-4,0)两点。
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)设此抛物线与直线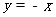 在第二象限交于点D,平行于
在第二象限交于点D,平行于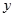 轴的直线
轴的直线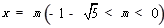 与抛物线交于点M,与直线
与抛物线交于点M,与直线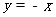 交于点N,连接BM、CM、NC、NB,是否存在
交于点N,连接BM、CM、NC、NB,是否存在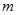 的值,使四边形BNCM的面积S最大?若存在,请求出
的值,使四边形BNCM的面积S最大?若存在,请求出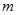 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25﹪,设每双鞋的成本价为 元.
元.
(1)试求 的值;
的值;
(2)为了扩大销售量,公司决定拿出一定量的资金做广告,根据市场调查,若每年投入广告费为 (万元)时,产品的年销售量将是原销售量的
(万元)时,产品的年销售量将是原销售量的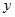 倍,且
倍,且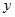 与
与 之间的关系如图所示,可近似看作是抛物线的一部分.
之间的关系如图所示,可近似看作是抛物线的一部分.
①根据图象提供的信息,求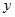 与
与 之间的函数关系式;
之间的函数关系式;
②求年利润 (万元)与广告费
(万元)与广告费 (万元)之间的函数关系式,并请回答广告费
(万元)之间的函数关系式,并请回答广告费 (万元)在什么范围内,公司获得的年利润
(万元)在什么范围内,公司获得的年利润 (万元)随广告费的增大而增多?(注:年利润
(万元)随广告费的增大而增多?(注:年利润 =年销售总额-成本费-广告费)
=年销售总额-成本费-广告费)