（本小题满分12分）为了了解某年段1000名学生的百米成绩情-优题课

题文

（本小题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.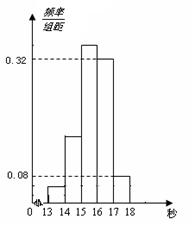

⑴将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
⑵求调查中随机抽取了多少个学生的百米成绩；
⑶若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.

科目数学题型解答题难度容易

登录免费查看答案和解析

相关试题

已知函数 $f (x) = \frac{\ln x + k}{e^{x}}$ （ $k$ 为常数， $e = 2.71828 . . .$ 是自然对数的底数），曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线与 $x$ 轴平行.
（Ⅰ）求 $k$ 的值；
（Ⅱ）求 $f (x)$ 的单调区间；
（Ⅲ）设 $g (x) = (x^{2} + x) f ` (x)$ ,其中 $f ` (x)$ 为 $f (x)$ 的导函数.证明：对任意 $x > 0, g (x) < 1 + e^{- 2}$ .

在平面直角坐标系 $x O y$ 中， $F$ 是抛物线 $C : x^{2} = 2 p y (p > 0)$ 的焦点， $M$ 是抛物线 $C$ 上位于第一象限内的任意一点，过 $M, F, O$ 三点的圆的圆心为 $Q$ ，点 $Q$ 到抛物线 $C$ 的准线的距离为 $\frac{3}{4}$ .
（Ⅰ）求抛物线 $C$ 的方程；
（Ⅱ）是否存在点 $M$ ，使得直线 $M Q$ 与抛物线 $C$ 相切于点 $M$ ？若存在，求出点 $M$ 的坐标；若不存在，说明理由；
（Ⅲ）若点 $M$ 的横坐标为 $\sqrt{2}$ ，直线 $l : y = k x + \frac{1}{4}$ 与抛物线 $C$ 有两个不同的交点 $A, B$ ， $l$ 与圆 $Q$ 有两个不同的交点 $D, E$ ，求当 $\frac{1}{2} \leq k \leq 2$ 时， ${|A B|}^{2} + {|D E|}^{2}$ 的最小值.

在等差数列 ${a_{n}}$ 中， $a_{3} + a_{4} + a_{5} = 84, a_{9} = 73$ .
（Ⅰ）求数列 ${a_{n}}$ 的通项公式；
（Ⅱ）对任意 $m \in N^{*}$ ，将数列 ${a_{n}}$ 中落入区间 $(9^{m}, 9^{2 m})$ 内的项的个数记为 $b_{m}$ ，求数列 ${b_{m}}$ 的前 $m$ 项和 $S_{m}$ .

先在甲、乙两个靶.某射手向甲靶射击一次，命中的概率为 $\frac{3}{4}$ ，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为 $\frac{2}{3}$ ,每命中一次得2分，没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
（Ⅰ）求该射手恰好命中一次的概率；
（Ⅱ）求该射手的总得分 $X$ 的分布列及数学期望 $E X$ .

在如图所示的几何体中，四边形 $A B C D$ 是等腰梯形， $A B$ $∥$ $C D$ ， $∠ D A B = 60^{°}, F C ⊥$ 平面 $A B C D, A E ⊥ B D, C B = C D$ .

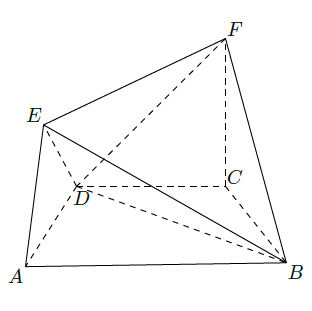
（Ⅰ）求证： $B D ⊥$ 平面 $A E D$ ；
（Ⅱ）求二面角 $F - B D - C$ 的余弦值.

试卷网试题网古诗词网作文网范文网