等差数列{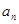 }前n项和为
}前n项和为 ,满足
,满足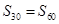 ,则下列结论中正确的是()
,则下列结论中正确的是()
A.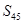 是 是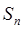 中的最大值 中的最大值 |
B.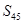 是 是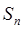 中的最小值 中的最小值 |
C.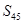 =0 =0 |
D. =0 =0 |
函数 的图象大致为()
的图象大致为()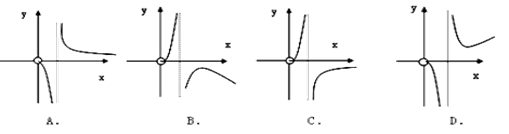
等差数列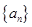 中,
中,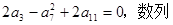
 为等比数列,且
为等比数列,且 ,则
,则 的值为()
的值为()
| A.4 | B.2 | C.16 | D.8 |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”,已知函数
的“隔离直线”,已知函数 ,有下列命题:
,有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为 ;
;
③ 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有()
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
已知定义域为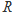 的奇函数
的奇函数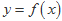 的导函数为
的导函数为 ,当
,当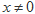 时
时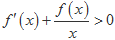
若 ,
,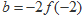 ,
,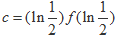 ,则
,则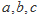 的大小关系是()
的大小关系是()
A.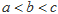 |
B.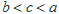 |
C. |
D.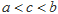 |