高温超导限流器由超导部件和限流电阻并联组成，如图所示。其中的超导部件有一个超导临界电流IC，当通过限流器的电流I>IC时，将造成超导体失超，即从超导态（电阻为零）转变成正常态（成为一个普通电阻），以此来限制电力系统的故障电流。已知超导部件成正常态时的电阻R1=3Ω，超导临界电流IC=1.2A，限流电阻R2=6Ω，小灯泡上标有“6V，6W”的字样，电源电动势E=8V，内阻r=2Ω，此时电路正常工作。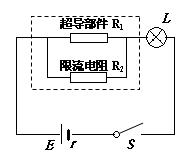
问：（1）求此时通过限流电阻R2的电流为多大；
（2）若L突然发生短路，则流过R2的电流为多大。
如图所示，一个质量为m、电荷量为q的正离子，在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中，磁场方向垂直纸面向里．结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场，此电场方向与AC平行且向上，最后离子打在G处，而G处距A点2d(AG⊥AC)．不计离子重力，离子运动轨迹在纸面内．求：
(1)此离子在磁场中做圆周运动的半径r；
(2)离子从D处运动到G处所需时间；
(3)离子到达G处时的动能．
如图所示，电阻R1＝2 Ω，小灯泡L上标有“3 V，1.5 W”字样，电源内阻r＝1 Ω，滑动变阻器的最大阻值为R0(大小未知)．当触头P滑动到最上端a时，电流表的读数为1 A，小灯泡L恰好正常发光，求：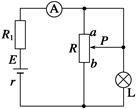
(1)滑动变阻器的最大阻值R0；
(2)当触头P滑动到最下端b时，电源的总功率及输出功率．
如图所示，在倾角θ＝30°的斜面上，固定一金属框，宽l＝0.25 m，接入电动势E＝12 V、内阻不计的电池．垂直框面放置一根质量m＝0.2 kg的金属棒ab，它与框架间的动摩擦因数μ＝
，整个装置放在磁感应强度B＝0.8 T、垂直框面向上的匀强磁场中。当调节滑动变阻器R的阻值在什么范围内时，可使金属棒静止在框架上？(框架与金属棒的电阻不计，g取10 m/s2)
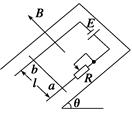
如图所示，光滑绝缘细杆竖直放置，细杆右侧距杆0.3m处有一固定的点电荷Q，A、B是细杆上的两点，点A与Q、点B与的连线与杆的夹角均为
=37°。一中间有小孔的带电小球穿在绝缘细杆上滑下，通过A 点时加速度为零，速度为3m/s，取g=10m/s2，求
（1）小球下落到B点时的加速度
（2）B点速度的大小。
如图所示为质谱仪的原理图，A为粒子加速器，电压为U1；B为速度选择器，磁场与电场正交，磁感应强度为B1，板间距离为d；C为偏转分离器，磁感应强度为B2。今有一质量为m、电量为q的正离子经加速后，恰好通过速度选择器，进入分离器后做半径为R的匀速圆周运动，求：
⑴粒子的速度v
⑵速度选择器的电压U2
⑶粒子在B2磁场中做匀速圆周运动的半径R。