已知万有引力常量为G，地球半径为R，同步卫星距地面的高度为h，地球的自转周期为T。某同学根据以上条件，提出一种计算地球赤道表面的物体随地球自转的线速度大小的方法：地球赤道表面的物体随地球作匀速圆周运动，由牛顿运动定律有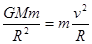
。又根据地球上的物体的重力与万有引力的关系，可以求得地球赤道表面的物体随地球自转的线速度的大小v。
（1）请判断上面的方法是否正确。如果正确，求出v的结果；如不正确，给出正确的解法和结果。
（2）由题目给出的条件再估算地球的质量。
用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块（可视为质点）。一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块，射穿后的速度v=100m/s，子弹与木块的作用时间极短，如图所示。g=10m/s2。求：
（1）在子弹打击木块的过程中系统（子弹与木块）产生的内能Q。
（2）打击后，木块上摆的最大高度H。
（3）
子弹射穿木块后的瞬间，木块所受绳的拉力T。
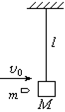
如图所示，倾斜挡板NM上有一个小孔K，NM与水平挡板NP成60°角，K与N间的距离
。现有质量为m，电荷量为q的正电粒子组成的粒子束，垂直于倾斜挡板NM，以速度v0不断射入，不计粒子所受的重力。
（1）若在NM和NP两档板所夹的区域内存在一个垂直于纸面向外的匀强磁场，NM和NP为磁场边界。粒子恰能垂直打在水平挡板NP上，求匀强磁场的磁感应强度的大小。
（2）若在NM和NP两档板所夹的区域内，只在某一部分区域存在一与（1）中大小相等方向相反的匀强磁场。从小孔K飞入的这些粒子经过磁场偏转后也能垂直打到水平挡板NP上（之前与挡板没有碰撞），求粒子在该磁场中运动的时间。
（3）若在（2）问中，磁感应强度大小未知，从小孔K飞入的这些粒子经过磁场偏转后能垂直打到水平挡板NP上（之前与挡板没有碰撞），求该磁场的磁感应强度的最小值。
如图所示，A、B、C三个物体质量均为m，其中厚度相同的A、B位于光滑的水平面上，可视为质点的小物块C放在静止的B物体上，物体A以速度v0向物体B运动，与B发生碰撞（碰撞时间极短），碰后A、B以相同的速度运动，但互不粘连；C滑过B后又在A上滑行，最后停在A上，与A一起以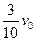
的速度运动。求：
（1）物体B最终的速度；
（2）小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比。
在一级方程式汽车大赛中，一辆赛车的总质量为m，一个路段的水平转弯半径为R，赛车转此弯时的速度为v，赛车形状都设计得使其上下方空气有一压力差——气动压力，从而增大了对地面的正压力。正压力与最大静摩擦力的比值叫侧向附着系数，以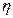
表示。要上述赛车转弯时不侧滑，则需要多大的气动压力？
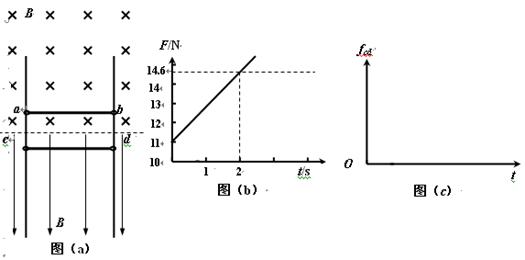
相距L＝1.5m的足够长金属导轨竖直放置，质量为m1＝1kg的金属棒ab和质量为m2＝0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0.75，两棒总电阻为1.8Ω，导轨电阻不计。ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放。
（1）指出在运动过程中ab棒中的电流方向和cd棒受到的安培力方向；
（2）求出磁感应强度B的大小和ab棒加速度大小；
（3）已知在2s内外力F做功40J，求这一过程中两金属棒产生的总焦耳热；
（4）判断cd棒将做怎样的运动，求出cd棒达到最大速度所需的时间t0，并在图（c）中定性画出cd棒所受摩擦力fcd随时间变化的图像。