有两个全等的等腰直角三角板ABC和EFG其直角边长均为6（如图1所示）叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点顺时针旋转，旋转角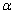
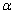满足0＜º＜90º，四边形CHGK是旋转过程中两块三角板的重叠部分（如图2）．
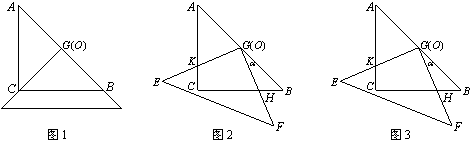
（1）在上述旋转过程中，①BH与CK有怎样的数量关系？②四边形CHGK的面积是否发生变化？并证明你发现的结论．
（2）如图，连接KH，在上述旋转过程中，是否存在某一位置使△GKH的面积恰好等于△ABC面积的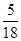
？若存在，请求出此时KC的长度；若不存在，请说明理由．
已知3b-2a-1=3a-2b，请利用等式性质比较a与b的大小．
某退休老师想为希望小学三年级（1）班的同学购买学习用品，了解到某商店每个书包的价格比每本词典多8元，用124元恰好可以买到3个书包和2本词典．
（1）每个书包和每本词典的价格各是多少元？
（2）老师计划用1000元为全班40位同学每人购买一件学习用品（一个书包或一本词典）后，余下不少于100元且不超过120元的钱购买体育用品，共有哪几种购买书包和词典的方案？
某地计划用120﹣180天（含120与180天）的时间建设一项水利工程，工程需要运送的土石方总量为360万米3．
（1）写出运输公司完成任务所需的时间y（单位：天）与平均每天的工作量x（单位：万米3）之间的函数关系式，并给出自变量x的取值范围；
（2）由于工程进度的需要，实际平均每天运送土石比原计划多5000米3，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少万米3？
如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．
（1）求AD的长；
（2）BC是⊙O的切线吗？若是，给出证明；若不是，说明理由．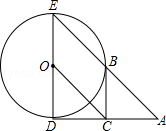
先化简，再求值：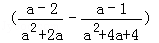
÷
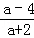，其中a=
﹣1．