一辆汽车从原点O出发沿x轴做直线运动,为研究汽车的运动而记下它在各时刻的位置和速度,见下表:
| 时刻t/s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 位置的坐标x/m |
0 |
0.5 |
2 |
4.5 |
8 |
12 |
16 |
20 |
| 瞬时速度v/(m·s-1) |
1 |
2 |
3 |
4 |
4 |
4 |
4 |
4 |
(1)汽车在第2 s末的瞬时速度为多少? (2)汽车在前3 s内的平均加速度为多少?
(3)汽车在第4 s内的平均速度为多少?
如图,光滑水平面上有三个物块A、B和C,它们具有相同的质量,且位于同一直线上。开始时,三个物块均静止,先让A以一定速度与B碰撞,碰后它们粘在一起,然后又一起与C碰撞并粘在一起,求前后两次碰撞中系统损失的动能之比。 
如图所示,一长为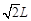 的木板,倾斜放置,倾角为45°,现有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板的夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球释放点距木板上端的水平距离为___________。
的木板,倾斜放置,倾角为45°,现有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板的夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球释放点距木板上端的水平距离为___________。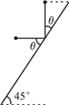
(1)在匀强磁场中,有一个原来静止的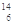 C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为()
C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为()
A.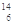 C → C → 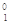 e+ e+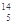 B B |
B.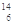 C → C → 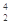 He+ He+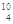 Be Be |
C.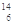 C → C → 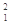 H+ H+ B B |
D.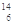 C → C → 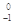 e+ e+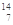 N N |
(2)如图所示,光滑水平面上有带有1/4光滑圆弧轨道的滑块,其质量为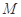 ,一质量为
,一质量为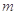 的小球,以速度
的小球,以速度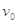 沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
(I)关于一定量的气体,下列说法正确的是
| A.气体的体积指的是该气体的分子所能到达的空间的体积,而不是该气体所有分子体积之和 |
| B.只要能减弱气体分子热运动的剧烈程度,气体的温度就可以降低 |
| C.在完全失重的情况下,气体对容器壁的压强为零 |
| D.气体从外界吸收热量,其内能一定增加 |
E.气体在等压膨胀过程中温度一定升高。
(2)如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长ll=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm。已知大气压强为P0=75.0cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为l'1=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。
如图所示,左右两边分别有两根平行金属导轨相距为L,左导轨与水平面夹30°角,右导轨与水平面夹60°角,左右导轨上端用导线连接。导轨空间内存在匀强磁场,左边的导轨处在方向沿左导轨平面向下,磁感应强度大小为B的磁场中。右边的导轨处在垂直于右导轨斜向上,磁感应强度大小也为B的磁场中。质量均为m的导杆ab和cd垂直导轨分别放于左右两侧导轨上,已知两导杆与两侧导轨间动摩擦因数均为μ=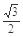 ,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑
,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑 距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。
距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。
(1)试求ab杆刚要开始运动时cd棒的速度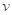
(2)以上过程中,回路中共产生多少焦耳热?
(3)cd棒的最终速度为多少?